1 Группы и преобразования .................................... 8
1.1 Группы: основные понятия и определения ..................... 8
1.1.1 Определение группы и подгруппы. Примеры ............. 8
1.1.2 Инвариантные подгруппы, смежные классы, фактор-
группа ............................................. 17
1.1.3 Прямое произведение групп, классы сопряженных
элементов, центр ................................... 20
1.1.4 Пример. Группа перестановок (симметрическая
группа) Sn. ........................................ 22
1.2 Матричные группы. Линейные, унитарные, ортогональные и
симплектические группы .................................... 28
1.2.1 Векторные пространства и алгебры ................... 28
1.2.2 Матрицы. Детерминант и пфаффиан .................... 30
1.2.3 Матричные группы и группы линейных преобразований
GL и SL ............................................ 35
1.2.4 Матричные группы, связанные с билинейными и
эрмитовыми формами ................................. 38
1.2.5 Матричные группы О, Sp и U типов ................... 41
1.3 Отображения. Группы и преобразования. Конформная группа ... 46
1.3.1 Понятие отображения ................................ 46
1.3.2 Гомоморфизм. Ядро и образ гомоморфизма ............. 48
1.3.3 Точные последовательности .......................... 50
1.3.4 Группы преобразований. Линейные неоднородные
группы ............................................. 52
1.3.5 Полупрямое произведение групп ...................... 55
1.3.6 Конформные группы Conf(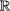 p,q) ....................... 58
2 Группы и алгебры Ли ....................................... 61
2.1 Многообразия. Группы Ли ................................... 62
2.1.1 Гладкие многообразия ............................... 62
2.1.2 Многообразия групп Ли. Примеры ..................... 68
2.1.3 Многообразия конформных групп Conf ( p,q) ....................... 58
2 Группы и алгебры Ли ....................................... 61
2.1 Многообразия. Группы Ли ................................... 62
2.1.1 Гладкие многообразия ............................... 62
2.1.2 Многообразия групп Ли. Примеры ..................... 68
2.1.3 Многообразия конформных групп Conf (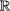 p,q).
Изоморфизм между Conf ( p,q).
Изоморфизм между Conf (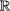 p,q) и O(р + 1, q + 1) ..... 75
2.1.4 Компактные группы Ли ............................... 79
2.1.5 Касательные пространства к гладким многообразиям ... 81
2.1.6 Инвариантная метрика на группе Ли. Мера Хаара ...... 86
2.2 Алгебры Ли ................................................ 92
2.2.1 Касательные пространства к многообразиям
матричных групп Ли ................................. 92
2.2.2 Матричные алгебры Ли ............................... 94
2.2.3 Примеры матричных алгебр Ли ........................ 96
2.2.4 Касательные пространства к многообразиям
матричных групп Ли (продолжение) .................. 103
2.2.5 Общее определение алгебр Ли. Гомоморфизмы алгебр
Ли. Экспоненциальное отображение p,q) и O(р + 1, q + 1) ..... 75
2.1.4 Компактные группы Ли ............................... 79
2.1.5 Касательные пространства к гладким многообразиям ... 81
2.1.6 Инвариантная метрика на группе Ли. Мера Хаара ...... 86
2.2 Алгебры Ли ................................................ 92
2.2.1 Касательные пространства к многообразиям
матричных групп Ли ................................. 92
2.2.2 Матричные алгебры Ли ............................... 94
2.2.3 Примеры матричных алгебр Ли ........................ 96
2.2.4 Касательные пространства к многообразиям
матричных групп Ли (продолжение) .................. 103
2.2.5 Общее определение алгебр Ли. Гомоморфизмы алгебр
Ли. Экспоненциальное отображение 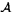 (G) → G ......... 104
2.2.6 Структурные соотношения. Простые и полупростые
алгебры Ли. Прямая сумма алгебр Ли ................ 110
2.2.7 Овеществления и вещественные формы комплексных
алгебр Ли ......................................... 114
2.2.8 Метрика Киллинга для алгебры Ли. Критерий
полупростоты ...................................... 119
2.2.9 Примеры структурных соотношений для некоторых
алгебр Ли ......................................... 122
2.2.10 Вещественные формы алгебр Ли sℓ (n, (G) → G ......... 104
2.2.6 Структурные соотношения. Простые и полупростые
алгебры Ли. Прямая сумма алгебр Ли ................ 110
2.2.7 Овеществления и вещественные формы комплексных
алгебр Ли ......................................... 114
2.2.8 Метрика Киллинга для алгебры Ли. Критерий
полупростоты ...................................... 119
2.2.9 Примеры структурных соотношений для некоторых
алгебр Ли ......................................... 122
2.2.10 Вещественные формы алгебр Ли sℓ (n,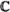 ), so(n. ), so(n.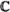 ) и
sp(2r,С) .......................................... 132
2.2.11 Алгебра Ли конформной группы Conf(]Rp'9) .......... 133
2.2.12 Изоморфизмы и автоморфизмы алгебр Ли: примеры.
Изоморфизмы алгебр so(3,C) = sℓ (2, ) и
sp(2r,С) .......................................... 132
2.2.11 Алгебра Ли конформной группы Conf(]Rp'9) .......... 133
2.2.12 Изоморфизмы и автоморфизмы алгебр Ли: примеры.
Изоморфизмы алгебр so(3,C) = sℓ (2,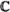 ), so(4, ), so(4,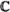 ) =
sℓ (2, ) =
sℓ (2,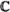 ) + sℓ (2, ) + sℓ (2,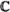 ), so(5, ), so(5,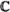 ) = sp(4, ) = sp(4,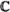 ),
so(6, ),
so(6,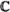 ) = sℓ (4, ) = sℓ (4,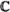 ) и их вещественных форм ......... 137
2.2.13 Локально изоморфные группы Ли. Универсальные
накрывающие ....................................... 147
3 Представления групп и представления алгебр Ли ............ 152
3.1 Линейные (матричные) представления групп ................. 152
3.1.1 Определение представления группы. Примеры ......... 152
3.1.2 Регулярные и индуцированные представления для
конечных групп. Точные и неточные представления ... 156
3.1.3 Эквивалентные представления. Эквивалентность
определяющего и сопряженного ему представлений
SU(2). Характер представления ..................... 160
3.2 Представления алгебр Ли .................................. 161
3.2.1 Определение представления алгебры Ли .............. 161
3.2.2 Примеры представлений алгебр Ли ................... 164
3.3 Прямое произведение и прямая сумма представлений ......... 166
3.3.1 Прямое (тензорное) произведение представлений.
Тензоры ........................................... 166
3.3.2 Прямая сумма представлений ........................ 170
3.4 Приводимые и неприводимые представления .................. 172
3.4.1 Определение приводимых и неприводимых
представлений ..................................... 172
3.4.2 Лемма Шура ........................................ 176
3.5 Некоторые свойства представлений конечных групп и
компактных групп Ли. Групповая алгебра и регулярные
представления ............................................ 181
3.6 Элементы теории характеров конечных групп и компактных
групп Ли ................................................. 186
3.6.1 Неприводимые представления и характеры групп С3
и S3 .............................................. 186
3.6.2 Свойства характеров конечных групп и компактных
групп Ли .......................................... 188
3.6.3 Неприводимые представления и характеры группы
SO(2) = U(1) ...................................... 195
3.7 Обертывающая алгебра. Операторы Казимира ................. 196
3.7.1 Определение обертывающей алгебры U( ) и их вещественных форм ......... 137
2.2.13 Локально изоморфные группы Ли. Универсальные
накрывающие ....................................... 147
3 Представления групп и представления алгебр Ли ............ 152
3.1 Линейные (матричные) представления групп ................. 152
3.1.1 Определение представления группы. Примеры ......... 152
3.1.2 Регулярные и индуцированные представления для
конечных групп. Точные и неточные представления ... 156
3.1.3 Эквивалентные представления. Эквивалентность
определяющего и сопряженного ему представлений
SU(2). Характер представления ..................... 160
3.2 Представления алгебр Ли .................................. 161
3.2.1 Определение представления алгебры Ли .............. 161
3.2.2 Примеры представлений алгебр Ли ................... 164
3.3 Прямое произведение и прямая сумма представлений ......... 166
3.3.1 Прямое (тензорное) произведение представлений.
Тензоры ........................................... 166
3.3.2 Прямая сумма представлений ........................ 170
3.4 Приводимые и неприводимые представления .................. 172
3.4.1 Определение приводимых и неприводимых
представлений ..................................... 172
3.4.2 Лемма Шура ........................................ 176
3.5 Некоторые свойства представлений конечных групп и
компактных групп Ли. Групповая алгебра и регулярные
представления ............................................ 181
3.6 Элементы теории характеров конечных групп и компактных
групп Ли ................................................. 186
3.6.1 Неприводимые представления и характеры групп С3
и S3 .............................................. 186
3.6.2 Свойства характеров конечных групп и компактных
групп Ли .......................................... 188
3.6.3 Неприводимые представления и характеры группы
SO(2) = U(1) ...................................... 195
3.7 Обертывающая алгебра. Операторы Казимира ................. 196
3.7.1 Определение обертывающей алгебры U(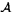 ) для
алгебры Ли ) для
алгебры Ли 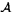 ...................................... 196
3.7.2 Представления алгебры U( ...................................... 196
3.7.2 Представления алгебры U(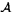 ). Центр алгебры U( ). Центр алгебры U(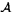 )
и операторы Казимира .............................. 199
3.7.3 Конечномерные представления алгебр Ли su(2) и
sℓ (2, )
и операторы Казимира .............................. 199
3.7.3 Конечномерные представления алгебр Ли su(2) и
sℓ (2, 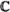 ) со старшим весом ........................ 209
3.7.4 Коумножение для обертывающей алгебры U( ) со старшим весом ........................ 209
3.7.4 Коумножение для обертывающей алгебры U(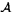 ).
Янгианы ........................................... 214
4 Компактные алгебры Ли .................................... 228
4.1 Определение и основные свойства компактных алгебр Ли ..... 228
4.2 Структура компактных алгебр Ли ........................... 231
4.3 Связь компактных алгебр Ли и компактных групп Ли ......... 234
4.4 Подалгебра Картана. Базис Картана-Вейля .................. 237
4.4.1 Регулярные элементы. Подалгебра Картана и ранг
алгебры Ли ........................................ 238
4.4.2 Базис Картана-Вейля ............................... 239
4.5 Корневые системы простых алгебр Ли ...................... 247
4.5.1 Свойства корней простых алгебр Ли ................. 247
4.5.2 Группа Вейля и простые корни ...................... 256
4.5.3 Диаграммы Дынкина. Корневые системы
классических алгебр Ли sℓ (n, ).
Янгианы ........................................... 214
4 Компактные алгебры Ли .................................... 228
4.1 Определение и основные свойства компактных алгебр Ли ..... 228
4.2 Структура компактных алгебр Ли ........................... 231
4.3 Связь компактных алгебр Ли и компактных групп Ли ......... 234
4.4 Подалгебра Картана. Базис Картана-Вейля .................. 237
4.4.1 Регулярные элементы. Подалгебра Картана и ранг
алгебры Ли ........................................ 238
4.4.2 Базис Картана-Вейля ............................... 239
4.5 Корневые системы простых алгебр Ли ...................... 247
4.5.1 Свойства корней простых алгебр Ли ................. 247
4.5.2 Группа Вейля и простые корни ...................... 256
4.5.3 Диаграммы Дынкина. Корневые системы
классических алгебр Ли sℓ (n,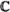 ), so(n, ), so(n,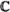 ),
sp(2n, ),
sp(2n,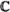 ) .......................................... 262
4.5.4 Диаграммы Дынкина для конечномерных простых
алгебр Ли. Классификация простых алгебр Ли ........ 273
4.5.5 Системы корней исключительных алгебр Ли .......... 280
5 Однородные пространства и их геометрия ................... 289
5.1 Однородные пространства .................................. 289
5.2 Примеры однородных пространств ........................... 293
5.3 Действие группы G на фактор-пространство G/H.
Индуцированные представления ............................. 301
5.4 Модели неевклидовой геометрии Лобачевского ............... 304
5.5 Метрика и оператор Лапласа на однородных пространствах ... 309
5.5.1 Элементы дифференциальной геометрии на гладких
многообразиях ..................................... 310
5.5.2 Инвариантная метрика на однородных
пространствах ..................................... 317
5.5.3 Регулярные представления и инвариантные
векторные поля на группах Ли ...................... 326
5.5.4 Операторы Лапласа на группах Ли и однородных
пространствах ..................................... 328
5.5.5 Сферические функции на однородных пространствах ... 332
6 Решения некоторых задач .................................. 335
6.1 Задача 8 раздела 1.1.1 ................................... 335
6.2 Задача 25 раздела 1.1.4 .................................. 335
6.3 Задача 54 раздела 1.2.5 .................................. 336
6.4 Задача 68 раздела 2.1.2 .................................. 337
6.5 Задача 77 раздела 2.2.2 .................................. 338
6.6 Задача 79 раздела 2.2.3 .................................. 341
6.7 Задача 119 раздела 2.2.12 ................................ 342
6.8 Задача 120 раздела 2.2.12 ................................ 343
6.9 Задача 121 раздела 2.2.12 ................................ 345
6.10 Задача 161 раздела 3.7.2 ................................. 348
6.11 Задача 197 раздела 4.5.5 ................................. 349
6.12 Задачи 198, 200 раздела 5.1 .............................. 350
6.13 Задача 219 раздела 5.5.2 ................................. 352
Литература .................................................... 354 ) .......................................... 262
4.5.4 Диаграммы Дынкина для конечномерных простых
алгебр Ли. Классификация простых алгебр Ли ........ 273
4.5.5 Системы корней исключительных алгебр Ли .......... 280
5 Однородные пространства и их геометрия ................... 289
5.1 Однородные пространства .................................. 289
5.2 Примеры однородных пространств ........................... 293
5.3 Действие группы G на фактор-пространство G/H.
Индуцированные представления ............................. 301
5.4 Модели неевклидовой геометрии Лобачевского ............... 304
5.5 Метрика и оператор Лапласа на однородных пространствах ... 309
5.5.1 Элементы дифференциальной геометрии на гладких
многообразиях ..................................... 310
5.5.2 Инвариантная метрика на однородных
пространствах ..................................... 317
5.5.3 Регулярные представления и инвариантные
векторные поля на группах Ли ...................... 326
5.5.4 Операторы Лапласа на группах Ли и однородных
пространствах ..................................... 328
5.5.5 Сферические функции на однородных пространствах ... 332
6 Решения некоторых задач .................................. 335
6.1 Задача 8 раздела 1.1.1 ................................... 335
6.2 Задача 25 раздела 1.1.4 .................................. 335
6.3 Задача 54 раздела 1.2.5 .................................. 336
6.4 Задача 68 раздела 2.1.2 .................................. 337
6.5 Задача 77 раздела 2.2.2 .................................. 338
6.6 Задача 79 раздела 2.2.3 .................................. 341
6.7 Задача 119 раздела 2.2.12 ................................ 342
6.8 Задача 120 раздела 2.2.12 ................................ 343
6.9 Задача 121 раздела 2.2.12 ................................ 345
6.10 Задача 161 раздела 3.7.2 ................................. 348
6.11 Задача 197 раздела 4.5.5 ................................. 349
6.12 Задачи 198, 200 раздела 5.1 .............................. 350
6.13 Задача 219 раздела 5.5.2 ................................. 352
Литература .................................................... 354
|