Preface ....................................................... vii
1 Introduction ................................................. 1
1.1 The four problems P, Pd, I, Id .......................... 2
1.2 Summary of content ...................................... 4
Part I Linear Integration and Linear Programming
2 The Linear Integration Problem I ............................. 9
2.1 Introduction ............................................ 9
2.2 Primal methods ......................................... 11
2.3 A dual approach ........................................ 15
2.4 A residue algorithm for problem I* ..................... 18
2.5 Notes .................................................. 29
3 Comparing the Continuous Problems P and I ................... 31
3.1 Introduction ........................................... 31
3.2 Comparing P, P*, I, and I* ............................. 33
3.3 Notes .................................................. 37
Part II Linear Counting and Integer Programming
4 The Linear Counting Problem Id .............................. 41
4.1 Introduction ........................................... 41
4.2 A primal approach: Barvinok's counting algorithm ....... 42
4.3 A dual approach ........................................ 45
4.4 Inversion of the 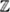 -transform by residues ............... 48
4.5 An algebraic method .................................... 52
4.6 A simple explicit formula .............................. 65
4.7 Notes .................................................. 69
5 Relating the Discrete Problems Pd and Id with P ............ 71
5.1 Introduction ........................................... 71
5.2 Comparing the dual problems I* and l*d ................. 72
5.3 A dual comparison of P and Pd .......................... 73
5.4 Proofs ................................................. 77
5.5 Notes .................................................. 79
Part III Duality
6 Duality and Gomory Relaxations .............................. 83
6.1 Introduction ........................................... 83
6.2 Gomory relaxations ..................................... 84
6.3 Brion and Vergne's formula and Gomory relaxations ...... 86
6.4 The Knapsack Problem ................................... 94
6.5 Adualof Pd ............................................. 96
6.6 Proofs ................................................. 99
6.7 Notes ................................................. 106
7 Barvinok's Counting Algorithm and Gomory Relaxations ....... 107
7.1 Introduction .......................................... 107
7.2 Solving Pd via Barvinok's counting algorithm ......... 108
7.3 The link with Gomory relaxations ...................... 111
7.4 Notes ................................................. 112
8 A Discrete Farkas Lemma .................................... 115
8.1 Introduction .......................................... 115
8.2 A discrete Farkas lemma ............................... 116
8.3 A discrete theorem of the alternative ................. 125
8.4 The knapsack equation ................................. 127
8.5 Notes ................................................. 129
9 The Integer Hull of a Convex Rational Polytope ............. 131
9.1 Introduction .......................................... 131
9.2 The integer hull ...................................... 132
9.3 Notes ................................................. 137
10 Duality and Superadditive Functions ........................ 139
10.1 Introduction .......................................... 139
10.2 Preliminaries ......................................... 140
10.3 Duality and superadditivity ........................... 142
10.4 Notes ................................................. 147
Appendix Legendre-Fenchel, Laplace, Cramer, and Z Transforms .. 149
A.l The Legendre-Fenchel transform ........................ 149
A.2 Laplace transform ..................................... 151
A.3 The Z-transform ....................................... 155
A.4 Notes ................................................. 157
References .................................................... 159
Glossary ...................................................... 165
Index ......................................................... 167
|
