Introduction .................................................... 1
Part I Introduction to fusion systems ........................... 5
1 The fusion category of a finite group ........................ 5
2 Abstract fusion systems ...................................... 7
3 Alperin's fusion theorem .................................... 11
4 Normal and central subgroups of a fusion system ............. 17
5 Normalizer fusion systems ................................... 21
6 Normal fusion subsystems and products ....................... 25
7 Fusion subsystems of p-power index or of index prime to p ... 32
8 The transfer homomorphism for saturated fusion systems ...... 38
9 Other definitions of saturation ............................. 45
Part II The local theory of fusion systems ..................... 49
1 Notation and terminology on groups .......................... 51
2 Fusion systems .............................................. 51
3 Saturated fusion systems .................................... 53
4 Models for constrained saturated fusion systems ............. 54
5 Factor systems and surjective morphisms ..................... 56
6 Invariant subsystems of fusion systems ...................... 60
7 Normal subsystems of fusion systems ......................... 62
8 Invariant maps and normal maps .............................. 65
9 Theorems on normal subsystems ............................... 68
10 Composition series .......................................... 71
11 Constrained systems ......................................... 78
12 Solvable systems ............................................ 80
13 Fusion systems in simple groups ............................. 84
14 Classifying simple groups and fusion systems ................ 87
15 Systems of characteristic 2-type ............................ 93
Part III Fusion and homotopy theory .......................... 103
1 Classifying spaces, p-completion, and the Martino-Priddy
conjecture ................................................. 106
1.1 Homotopy and fundamental groups ....................... 106
1.2 CW complexes and cellular homology .................... 109
1.3 Classifying spaces of discrete groups ................. 110
1.4 The p-completion functor of Bousfield and Kan ......... 113
1.5 Equivalences between fusion systems of finite groups .. 116
1.6 The Martino-Priddy conjecture ......................... 117
1.7 An application: fusion in finite groups of Lie type ... 118
2 The geometric realization of a category .................... 119
2.1 Simplicial sets and their realizations ................ 120
2.2 The nerve of a category as a simplicial set ........... 122
2.3 Classifying spaces as geometric realizations of
categories ............................................ 124
2.4 Fundamental groups and coverings of geometric
realizations .......................................... 125
2.5 Spaces of maps ........................................ 129
3 Linking systems and classifying spaces of finite groups .... 133
3.1 The linking category of a finite group ................ 133
3.2 Fusion and linking categories of spaces ............... 135
3.3 Linking systems and equivalences of p-completed
classifying spaces .................................... 138
4 Abstract fusion and linking systems ........................ 139
4.1 Linking systems, centric linking systems and p-local
finite groups ......................................... 140
4.2 Quasicentric subgroups and quasicentric linking
systems ............................................... 143
4.3 Automorphisms of fusion and linking systems ........... 152
4.4 Normal fusion and linking subsystems .................. 155
4.5 Fundamental groups and covering spaces ................ 158
4.6 Homotopy properties of classifying spaces ............. 161
4.7 Classifying spectra of fusion systems ................. 165
4.8 An infinite version: p-local compact groups ........... 167
5 The orbit category and its applications .................... 168
5.1 Higher limits of functors and the bar resolution ...... 170
5.2 Constrained fusion systems ............................ 175
5.3 Existence, uniqueness, and automorphisms of linking
systems ............................................... 182
5.4 Some computational techniques for higher limits over
orbit categories ...................................... 189
5.5 Homotopy colimits and homotopy decompositions ......... 197
5.6 The subgroup decomposition of |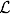 | ..................... 200
5.7 An outline of the proofs of Theorems 4.21 and 4.22 .... 204
5.8 The centralizer and normalizer decompositions of | | ..................... 200
5.7 An outline of the proofs of Theorems 4.21 and 4.22 .... 204
5.8 The centralizer and normalizer decompositions of |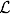 | .. 207
6 Examples of exotic fusion systems .......................... 209
6.1 Reduced fusion systems and tame fusion systems ........ 210
6.2 The Ruiz-Viruel examples .............................. 212
6.3 Saturated fusion systems over 2-groups ................ 214
6.4 Mixing related fusion systems ......................... 215
6.5 Other examples ........................................ 215
7 Open problems .............................................. 216
Part IV Fusion and Representation theory ..................... 220
1 Algebras and G-algebras .................................... 222
1.1 Ideals and Idempotents ................................ 222
1.2 G-algebras ............................................ 226
1.3 Relative trace maps and Brauer homomorphisms .......... 227
2 p-permutation algebras, Brauer pairs and fusion systems .... 232
2.1 p-permutation algebras and the Brauer homomorphisms ... 232
2.2 (A, G)-Brauer pairs and inclusion ..................... 235
2.3 (A, b, G)-Brauer pairs and inclusion .................. 241
2.4 (A, b, G)-Brauer pairs and fusion systems ............. 243
3 p-permutation algebras and saturated fusion systems ........ 244
3.1 Saturated triples ..................................... 244
3.2 Normaliser systems and saturated triples .............. 249
3.3 Saturated triples and normal subgroups ................ 251
3.4 Block fusion systems .................................. 253
3.5 Fusion systems of blocks of local subgroups ........... 255
4 Background on finite group representations ................. 258
4.1 Ordinary and modular representations .................. 259
4.2 p-modular systems ..................................... 261
4.3 Cartan and decomposition maps ......................... 262
4.4 Ordinary and Brauer characters ........................ 266
5 Fusion and structure ....................................... 270
5.1 The three main theorems of Brauer ..................... 270
5.2 Relative projectivity and representation type ......... 274
5.3 Finiteness conjectures ................................ 276
5.4 Source algebras and Puig's conjecture ................. 278
5.5 Kьlshammer-Puig classes ............................... 281
5.6 Nilpotent blocks and extensions ....................... 286
5.7 Counting Conjectures .................................. 288
6 Block fusion systems and normal subgroups .................. 293
7 Open Problems .............................................. 298
Appendix A. Background facts about groups ..................... 300
References .................................................... 306
List of notation .............................................. 314
Index ......................................................... 317 | .. 207
6 Examples of exotic fusion systems .......................... 209
6.1 Reduced fusion systems and tame fusion systems ........ 210
6.2 The Ruiz-Viruel examples .............................. 212
6.3 Saturated fusion systems over 2-groups ................ 214
6.4 Mixing related fusion systems ......................... 215
6.5 Other examples ........................................ 215
7 Open problems .............................................. 216
Part IV Fusion and Representation theory ..................... 220
1 Algebras and G-algebras .................................... 222
1.1 Ideals and Idempotents ................................ 222
1.2 G-algebras ............................................ 226
1.3 Relative trace maps and Brauer homomorphisms .......... 227
2 p-permutation algebras, Brauer pairs and fusion systems .... 232
2.1 p-permutation algebras and the Brauer homomorphisms ... 232
2.2 (A, G)-Brauer pairs and inclusion ..................... 235
2.3 (A, b, G)-Brauer pairs and inclusion .................. 241
2.4 (A, b, G)-Brauer pairs and fusion systems ............. 243
3 p-permutation algebras and saturated fusion systems ........ 244
3.1 Saturated triples ..................................... 244
3.2 Normaliser systems and saturated triples .............. 249
3.3 Saturated triples and normal subgroups ................ 251
3.4 Block fusion systems .................................. 253
3.5 Fusion systems of blocks of local subgroups ........... 255
4 Background on finite group representations ................. 258
4.1 Ordinary and modular representations .................. 259
4.2 p-modular systems ..................................... 261
4.3 Cartan and decomposition maps ......................... 262
4.4 Ordinary and Brauer characters ........................ 266
5 Fusion and structure ....................................... 270
5.1 The three main theorems of Brauer ..................... 270
5.2 Relative projectivity and representation type ......... 274
5.3 Finiteness conjectures ................................ 276
5.4 Source algebras and Puig's conjecture ................. 278
5.5 Kьlshammer-Puig classes ............................... 281
5.6 Nilpotent blocks and extensions ....................... 286
5.7 Counting Conjectures .................................. 288
6 Block fusion systems and normal subgroups .................. 293
7 Open Problems .............................................. 298
Appendix A. Background facts about groups ..................... 300
References .................................................... 306
List of notation .............................................. 314
Index ......................................................... 317
|