Preface ........................................................ ix
Part I. Topological Vector Spaces. Spaces of Functions .......... 2
1 Filters. Topological Spaces. Continuous Mappings ............. 6
2 Vector Spaces. Linear Mappings .............................. 14
3 Topological Vector Spaces. Definition ....................... 20
4 Hausdorff Topological Vector Spaces. Quotient Topological
Vector Spaces. Continuous Linear Mappings ................... 31
Hausdorff Topological Vector Spaces ......................... 31
Quotient Topological Vector Spaces .......................... 33
Continuous Linear Mappings .................................. 34
5 Cauchy Filters. Complete Subsets. Completion ................ 37
6 Compact Sets ................................................ 50
7 Locally Convex Spaces. Seminorms ............................ 57
8 Metrizable Topological Vector Spaces ........................ 70
9 Finite Dimensional Hausdorff Topological Vector Spaces.
Linear Subspaces with Finite Codimension. Hyperplanes ....... 78
10 Frechet Spaces. Examples .................................... 85
Example I. The Space of 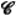 k Functions in a Open Subset Ω
of Rn ....................................................... 85
Example II. The Space of Holomorphic Functions in an
Open Subset Ω of Cn ......................................... 89
Example III. The Space of Formal Power Series in
n Indeterminates ............................................ 91
Example IV. The Space k Functions in a Open Subset Ω
of Rn ....................................................... 85
Example II. The Space of Holomorphic Functions in an
Open Subset Ω of Cn ......................................... 89
Example III. The Space of Formal Power Series in
n Indeterminates ............................................ 91
Example IV. The Space 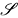 of of 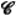 ∞ Functions in Rn, Rapidly
Decreasing at Infinity ...................................... 92
11 Normable Spaces. Banach Spaces. Examples .................... 95
12 Hilbert Spaces ............................................. 112
13 Spaces LF. Examples ........................................ 126
14 Bounded Sets ............................................... 136
15 Approximation Procedures in Spaces of Functions ............ 150
16 Partitions of Unity ........................................ 161
17 The Open Mapping Theorem ................................... 166
Part II. Duality. Spaces of Distributions ..................... 175
18 The Hahn-Banach Theorem .................................... 181
(1) Problems of Approximation .............................. 186
(2) Problems of Existence .................................. 187
(3) Problems of Separation ................................. 189
19 Topologies on the Dual ..................................... 195
20 Examples of Duals among Lp Spaces .......................... 202
Example I. The Duals of the Spaces of Sequences lp
(1 ≤ p < +∞) ............................................... 206
Example II. The Duals of the Spaces Lp(Ω) (1 ≤ p < +∞) ..... 210
21 Radon Measures. Distributions .............................. 216
Radon Measures in an Open Subset of Rn ..................... 216
Distributions in an Open Subset of Rn ...................... 222
22 More Duals: Polynomials and Formal Power Series.
Analytic Functionals ....................................... 227
Polynomials and Formal Power Series ........................ 227
Analytic Functionals in an Open Subset Ω of Cn ............. 231
23 Transpose of a Continuous Linear Map ....................... 240
Example I. Injections of Duals ............................. 243
Example II. Restrictions and Extensions .................... 245
Example III. Differential Operators ........................ 247
24 Support and Structure of a Distribution .................... 253
Distributions with Support at the Origin ................... 264
25 Example of Transpose: Fourier Transformation of Tempered
Distributions .............................................. 267
26 Convolution of Functions ................................... 278
27 Example of Transpose: Convolution of Distributions ......... 284
28 Approximation of Distributions by Cutting and
Regularizing ............................................... 298
29 Fourier Transforms of Distributions with Compact Support.
The Paley-Wiener Theorem ................................... 305
30 Fourier Transforms of Convolutions and Multiplications ..... 314
31 The Sobolev Spaces ......................................... 322
32 Equicontinuous Sets of Linear Mappings ..................... 335
33 Barreled Spaces. The Banach-Steinhaus Theorem .............. 346
34 Applications of the Banach-Steinhaus Theorem ............... 351
34.1 Application to Hilbert Spaces ......................... 351
34.2 Application to Separately Continuous Functions on
Products .............................................. 352
34.3 Complete Subsets of L ∞ Functions in Rn, Rapidly
Decreasing at Infinity ...................................... 92
11 Normable Spaces. Banach Spaces. Examples .................... 95
12 Hilbert Spaces ............................................. 112
13 Spaces LF. Examples ........................................ 126
14 Bounded Sets ............................................... 136
15 Approximation Procedures in Spaces of Functions ............ 150
16 Partitions of Unity ........................................ 161
17 The Open Mapping Theorem ................................... 166
Part II. Duality. Spaces of Distributions ..................... 175
18 The Hahn-Banach Theorem .................................... 181
(1) Problems of Approximation .............................. 186
(2) Problems of Existence .................................. 187
(3) Problems of Separation ................................. 189
19 Topologies on the Dual ..................................... 195
20 Examples of Duals among Lp Spaces .......................... 202
Example I. The Duals of the Spaces of Sequences lp
(1 ≤ p < +∞) ............................................... 206
Example II. The Duals of the Spaces Lp(Ω) (1 ≤ p < +∞) ..... 210
21 Radon Measures. Distributions .............................. 216
Radon Measures in an Open Subset of Rn ..................... 216
Distributions in an Open Subset of Rn ...................... 222
22 More Duals: Polynomials and Formal Power Series.
Analytic Functionals ....................................... 227
Polynomials and Formal Power Series ........................ 227
Analytic Functionals in an Open Subset Ω of Cn ............. 231
23 Transpose of a Continuous Linear Map ....................... 240
Example I. Injections of Duals ............................. 243
Example II. Restrictions and Extensions .................... 245
Example III. Differential Operators ........................ 247
24 Support and Structure of a Distribution .................... 253
Distributions with Support at the Origin ................... 264
25 Example of Transpose: Fourier Transformation of Tempered
Distributions .............................................. 267
26 Convolution of Functions ................................... 278
27 Example of Transpose: Convolution of Distributions ......... 284
28 Approximation of Distributions by Cutting and
Regularizing ............................................... 298
29 Fourier Transforms of Distributions with Compact Support.
The Paley-Wiener Theorem ................................... 305
30 Fourier Transforms of Convolutions and Multiplications ..... 314
31 The Sobolev Spaces ......................................... 322
32 Equicontinuous Sets of Linear Mappings ..................... 335
33 Barreled Spaces. The Banach-Steinhaus Theorem .............. 346
34 Applications of the Banach-Steinhaus Theorem ............... 351
34.1 Application to Hilbert Spaces ......................... 351
34.2 Application to Separately Continuous Functions on
Products .............................................. 352
34.3 Complete Subsets of L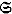 (E; F) .......................... 354
34.4 Duals of Montel Spaces ................................ 356
35 Further Study of the Weak Topology ......................... 360
36 Topologies Compatible with a Duality. The Theorem of
Mackey. Reflexivity ........................................ 368
The Normed Space EB ........................................ 370
Examples of Semireflexive and Reflexive Spaces ............. 374
37 Surjections of Frechet Spaces .............................. 378
Proof of Theorem 37.1 ...................................... 379
Proof of Theorem 37.2 ...................................... 383
38 Surjections of Frechet Spaces (continued). Applications .... 387
Proof of Theorem 37.3 ...................................... 387
An Application of Theorem 37.2: A Theorem of E. Borel ...... 390
An Application of Theorem 37.3: A Theorem of Existence of (E; F) .......................... 354
34.4 Duals of Montel Spaces ................................ 356
35 Further Study of the Weak Topology ......................... 360
36 Topologies Compatible with a Duality. The Theorem of
Mackey. Reflexivity ........................................ 368
The Normed Space EB ........................................ 370
Examples of Semireflexive and Reflexive Spaces ............. 374
37 Surjections of Frechet Spaces .............................. 378
Proof of Theorem 37.1 ...................................... 379
Proof of Theorem 37.2 ...................................... 383
38 Surjections of Frechet Spaces (continued). Applications .... 387
Proof of Theorem 37.3 ...................................... 387
An Application of Theorem 37.2: A Theorem of E. Borel ...... 390
An Application of Theorem 37.3: A Theorem of Existence of
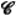 ∞ Solutions of a Linear Partial Differential Equation ..... 391
Part III. Tensor Products. Kernels ............................ 395
39 Tensor Product of Vector Spaces ............................ 403
40 Differentiable Functions with Values in Topological Vector
Spaces. Tensor Product of Distributions .................... 411
41 Bilinear Mappings. Hypocontinuity .......................... 420
Proof of Theorem 41.1 ...................................... 421
42 Spaces of Bilinear Forms. Relation with Spaces of Linear
Mappings and with Tensor Products .......................... 427
43 The Two Main Topologies on Tensor Products. Completion of
Topological Tensor Products ................................ 434
44 Examples of Completion of Topological Tensor Products:
Products ε ................................................. 446
Example 44.1. The Space ∞ Solutions of a Linear Partial Differential Equation ..... 391
Part III. Tensor Products. Kernels ............................ 395
39 Tensor Product of Vector Spaces ............................ 403
40 Differentiable Functions with Values in Topological Vector
Spaces. Tensor Product of Distributions .................... 411
41 Bilinear Mappings. Hypocontinuity .......................... 420
Proof of Theorem 41.1 ...................................... 421
42 Spaces of Bilinear Forms. Relation with Spaces of Linear
Mappings and with Tensor Products .......................... 427
43 The Two Main Topologies on Tensor Products. Completion of
Topological Tensor Products ................................ 434
44 Examples of Completion of Topological Tensor Products:
Products ε ................................................. 446
Example 44.1. The Space 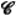 m(X; E) of m(X; E) of 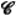 m Functions Valued in
a Locally Convex Hausdorff Space E
(0 ≤ m ≤ +∞) ................................. 446
Example 44.2. Summable Sequences in a Locally Convex
Hausdorff Space .............................. 451
45 Examples of Completion of Topological Tensor Products:
Completed π-Product of Two Fréchet Spaces .................. 459
46 Examples of Completion of Topological Tensor Products:
Completed π-Products with a Space L1 ....................... 467
46.1 The Spaces Lα(E) ...................................... 467
46.2 The Theorem of Dunford-Pettis ......................... 469
46.3 Application to L1 m Functions Valued in
a Locally Convex Hausdorff Space E
(0 ≤ m ≤ +∞) ................................. 446
Example 44.2. Summable Sequences in a Locally Convex
Hausdorff Space .............................. 451
45 Examples of Completion of Topological Tensor Products:
Completed π-Product of Two Fréchet Spaces .................. 459
46 Examples of Completion of Topological Tensor Products:
Completed π-Products with a Space L1 ....................... 467
46.1 The Spaces Lα(E) ...................................... 467
46.2 The Theorem of Dunford-Pettis ......................... 469
46.3 Application to L1  π E ................................ 473
47 Nuclear Mappings ........................................... 477
Example. Nuclear Mappings of a Banach Space into a Space
L1 ................................................ 486
48 Nuclear Operators in Hilbert Spaces ........................ 488
49 The Dual of E π E ................................ 473
47 Nuclear Mappings ........................................... 477
Example. Nuclear Mappings of a Banach Space into a Space
L1 ................................................ 486
48 Nuclear Operators in Hilbert Spaces ........................ 488
49 The Dual of E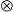 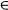 F, Integral Mappings ........................ 500
50 Nuclear Spaces ............................................. 509
Proof of Proposition 50.1 .................................. 516
51 Examples of Nuclear Spaces. The Kernels Theorem ............ 526
52 Applications ............................................... 535
Appendix: The Borel Graph Theorem .......................... 549
Bibliography for Appendix .................................. 557
General Bibliography ....................................... 558
Index of Notation ............................................. 559
Subject Index ................................................. 561 F, Integral Mappings ........................ 500
50 Nuclear Spaces ............................................. 509
Proof of Proposition 50.1 .................................. 516
51 Examples of Nuclear Spaces. The Kernels Theorem ............ 526
52 Applications ............................................... 535
Appendix: The Borel Graph Theorem .......................... 549
Bibliography for Appendix .................................. 557
General Bibliography ....................................... 558
Index of Notation ............................................. 559
Subject Index ................................................. 561
|