Preface ........................................................ ix
Introduction .................................................... 1
Definitions, notation, and some standard facts ................. 13
I Background .................................................. 21
1 Classical Calderón-Zygmund decomposition and real
interpolation ............................................... 23
1.1 Riesz rising sun lemma and the Calderón-Zygmund
procedure .............................................. 23
1.1.1 Riesz rising sun lemma .......................... 23
1.1.2 Calderón-Zygmund lemma .......................... 25
1.1.3 Calderón-Zygmund decomposition .................. 26
1.1.4 A weak type inequality for linear operators ..... 29
1.1.5 Hardy-Littlewood maximal operator ............... 31
1.2 Norms on BMO and Lipschitz spaces ...................... 33
1.2.1 John-Nirenberg inequality ....................... 34
1.2.2 Equivalence of Campanato norms .................. 36
1.3 Relationship with real interpolation ................... 39
1.4 An elementary stability theorem ........................ 42
1.4.1 A proof with much interpolation ................. 42
1.4.2 Stabilization à la Bourgain ..................... 43
1.4.3 Some consequences ............................... 44
Notes and remarks ........................................... 45
2 Singular integrals .......................................... 47
2.1 Hilbert transformation ................................. 48
2.1.1 Hilbert transformation on L1 .................... 50
2.1.2 The operator H on Lp, 1 < p < ∞ ................. 51
2.2 General definition ..................................... 52
2.2.1 Examples ........................................ 54
2.2.2 Additional information .......................... 61
2.3 Vector-valued analogs .................................. 62
Notes and remarks ........................................... 64
3 Classical covering theorems ................................. 65
3.1 Classical covering theorems and partitions of unity .... 65
3.1.1 The Besicovitch q-process ....................... 65
3.1.2 Besicovitch theorem ............................. 67
3.1.3 Wiener lemma .................................... 70
3.1.4 Whitney lemma, WB-coverings, and partitions of
unity ........................................... 71
3.2 Another Calderon Zygmund procedure ..................... 77
3.3 Stability of near-minimizers for the couple (L1,
L∞) .................................................... 82
3.3.1 Statement and proof ............................. 82
3.3.2 Vector form of the stability theorem ............ 86
Notes and remarks ........................................... 89
4 Spaces of smooth functions and operators on them ............ 91
4.1 Summary ................................................ 91
4.1.1 Homogeneous spaces of smooth functions .......... 91
4.1.2 Singular integral operators ..................... 95
4.2 Morrey-Campanato spaces: proofs ........................ 97
4.3 BMO and atomic H1 ..................................... 102
4.4 Continuity of operators on BMO and Lipschitz spaces ... 106
4.4.1 A pointwise estimate ........................... 108
4.4.2 Norm estimates ................................. 112
4.5 Singular integrals related to wavelet expansions ...... 114
4.5.1 More general operators ......................... 115
4.5.2 Consequences ................................... 118
4.5.3 An omitted proof ............................... 118
4.6 Weak L1-boundedness ................................... 120
Notes and remarks .......................................... 121
5 Some topics in interpolation ............................... 123
5.1 Main notions .......................................... 123
5.2 Near-minimizers and interpolation ..................... 127
5.3 Near-minimizers for Lp,q- and К-functional ............ 129
5.4 Near-minimizers for E- and K-functionals .............. 131
5.5 The elementary stability theorem revisited ............ 135
5.6 K-closed subcouples and stability ..................... 136
5.7 Linearization ......................................... 141
Notes and remarks .......................................... 143
6 Regularization for Banach spaces ........................... 145
Notes and remarks .......................................... 150
7 Stability for analytic Hardy spaces ........................ 153
Notes and remarks .......................................... 155
II Advanced theory ........................................... 159
8 Controlled coverings ....................................... 161
8.1 Whitney lemma and a theorem about Lipschitz
families .............................................. 163
8.1.1 Auxiliary lemmas ............................... 166
8.1.2 Finite overlap ................................. 167
8.1.3 Meshing algorithm and the strong engagement
lemma .......................................... 169
8.1.4 Modified Besicovitch q-process ................. 171
8.1.5 Proof of Theorem 8.16 .......................... 172
8.1.6 Proof of Theorem 8.9 ........................... 173
8.1.7 Proof of Theorem 8.13 .......................... 174
8.2 Controlled extension and preservation of the
α-capacity ............................................ 175
8.2.1 The Besicovitch process with a Lipschitz
condition ...................................... 177
8.2.2 Construction of a WB-covering .................. 180
8.2.3 Proof of the controlled extension theorem ...... 183
8.2.4 Proof of the theorem on the preservation of
α-capacity for α 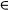 (1 - 1/n, 1) ................ 185
8.3 Controlled contraction and preservation of the
α-capacity ............................................ 186
8.3.1 Besicovitch q-process with a Lipschitz
condition for controlled contraction ........... 188
8.3.2 Construction of a WB-covering .................. 190
8.3.3 Proof of the contraction theorem ............... 191
8.4 Preservation of the α-capacity (α < 0) ................ 194
Notes and remarks .......................................... 196
9 Construction of near-minimizers ............................ 197
9.1 Estimates for derivatives of approximants ............. 198
9.2 Near-minimizers for Sobolev spaces: the couples
(Lp, Wkq) ............................................. 200
9.2.1 Near-minimizers for the couple (Lp, Wkp) ....... 201
9.2.2 Near-minimizers for the couple (Lp, Wkq) when
q ≠ p .......................................... 205
9.2.3 Statement and proof of the main result ......... 209
9.3 Near-minimizers for Morrey-Campanato spaces: the
couples (Lp, Ċα,kp) ................................... 212
9.3.1 Algorithm for constructing near-minimizers ..... 213
9.3.2 Statement and the proof of the main result ..... 214
Notes and remarks .......................................... 219
10 Stability of near-minimizers ............................... 221
10.1 Construction of approximating polynomials ............. 222
10.2 Stability theorems: statements and applications ....... 227
10.2.1 Statements ..................................... 227
10.2.2 Applications ................................... 229
10.3 Proof of Theorems 10.4-10.6 ........................... 232
10.3.1 Proof of the main lemma ........................ 236
Notes and remarks .......................................... 241
11 The omitted case of a limit exponent ....................... 243
11.1 Description of the algorithm .......................... 244
11.2 Principal results, and outlines of the proofs ......... 247
11.2.1 Statement of the main results .................. 247
11.3 Proofs ................................................ 249
11.3.1 The case of t ≥ t* ............................. 249
11.3.2 Lemmas valid in the multidimensional case
and Theorem 11.3 ............................... 251
11.3.3 Geometric lemmas and the proofs of Theorems
11.4 and 11.5 .................................. 255
Notes and remarks .......................................... 272
A Appendix. Near-minimizers for Brudnyi and Triebel-
Lizorkin spaces ............................................ 273
A.l Description of the general algorithm .................. 273
A.2 Morrey spaces built on Brudnyi spaces ................. 276
A.2.1 Auxiliary lemmas ............................... 279
A.2.2 Proof of the main result (Theorem A.3) ......... 285
A.3 Morrey spaces built on Triebel-Lizorkin spaces ......... 291
A.3.1 Auxiliary lemmas ............................... 293
A.3.2 Proof of the main result (Theorem A. 12) ....... 300
Notes and remarks ............................................. 304
Bibliography .................................................. 305
Index ......................................................... 313
|
