Preface ........................................................ ix
Introduction .................................................... 1
Chapter 1 Semiflows on Metric Spaces ........................... 9
§1.1 Metric spaces ............................................. 9
§1.2 Semiflows ................................................ 17
§1.3 Invariant sets ........................................... 19
§1.4 Exercises ................................................ 25
Chapter 2 Compact Attractors .................................. 29
§2.1 Compact attractors of individual sets .................... 30
§2.2 Compact attractors of classes of sets .................... 36
§2.3 A sufficient condition for asymptotic smoothness ......... 51
§2.4 a-limit sets of total trajectories ....................... 52
§2.5 Invariant sets identified through Lyapunov functions ..... 52
§2.6 Discrete semiflows induced by weak contractions .......... 54
§2.7 Exercises ................................................ 57
Chapter 3 Uniform Weak Persistence ............................ 61
§3.1 Persistence definitions .................................. 61
§3.2 An SEIRS epidemic model in patchy host populations ....... 64
§3.3 Nonlinear matrix models: Prolog .......................... 71
§3.4 The May-Leonard example of cyclic competition ............ 78
§3.5 Exercises ................................................ 84
Chapter 4 Uniform Persistence ................................. 87
§4.1 From uniform weak to uniform persistence ................. 87
§4.2 From uniform weak to uniform persistence: Discrete
case ..................................................... 91
§4.3 Application to a metered endemic model of SIR type ....... 94
§4.4 From uniform weak to uniform persistence for time-set
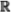 + ....................................................... 97
§4.5 Persistence a la Baron von Munchhausen ................... 99
§4.6 Navigating between alternative persistence functions .... 107
§4.7 A fertility reducing endemic with two stages of
infection ............................................... 110
§4.8 Exercises ............................................... 123
Chapter 5 The Interplay of Attractors, Repellers, and
Persistence ........................................ 125
§5.1 An attractor of points facilitates persistence .......... 125
§5.2 Partition of the global attractor under uniform
persistence ............................................. 127
§5.3 Repellers and dual attractors ........................... 135
§5.4 The cyclic competition model of May and Leonard
revisited ............................................... 139
§5.5 Attractors at the brink of extinction ................... 140
§5.6 An attractor under two persistence functions ............ 141
§5.7 Persistence of bacteria and phages in a chemostat ....... 142
§5.8 Exercises ............................................... 155
Chapter 6 Existence of Nontrivial Fixed Points via
Persistence ........................................ 157
§6.1 Nontrivial fixed points in the global compact
attractor ............................................... 158
§6.2 Periodic solutions of the Lotka-Volterra predator-prey
model ................................................... 160
§6.3 Exercises ............................................... 162
Chapter 7 Nonlinear Matrix Models: Main Act .................. 163
§7.1 Forward invariant balls and compact attractors of
bounded sets ............................................ 163
§7.2 Existence of nontrivial fixed points .................... 165
§7.3 Uniform persistence and persistence attractors .......... 167
§7.4 Stage persistence ....................................... 171
§7.5 Exercises ............................................... 175
Chapter 8 Topological Approaches to Persistence .............. 177
§8.1 Attractors and repellers ................................ 177
§8.2 Chain transitivity and the Butler-McGehee lemma ......... 180
§8.3 Acyclicity implies uniform weak persistence ............. 185
§8.4 Uniform persistence in a food chain ..................... 191
§8.5 The metered endemic model revisited ..................... 196
§8.6 Nonlinear matrix models (epilog): Biennials ............. 199
§8.7 An endemic with vaccination and temporary immunity ...... 209
§8.8 Lyapunov exponents and persistence for ODEs and maps .... 215
§8.9 Exercises ............................................... 229
Chapter 9 An SI Endemic Model with Variable Infectivity ...... 231
§9.1 The model ............................................... 231
§9.2 Host persistence and disease extinction ................. 236
§9.3 Uniform weak disease persistence ........................ 237
§9.4 The semiflow ............................................ 239
§9.5 Existence of a global compact attractor ................. 240
§9.6 Uniform disease persistence ............................. 245
§9.7 Disease extinction and the disease-free equilibrium ..... 247
§9.8 The endemic equilibrium ................................. 249
§9.9 Persistence as a crossroad to global stability .......... 250
§9.10 Measure-valued distributions of infection-age ........... 254
Chapter 10 Semiflows Induced by Semilinear Cauchy Problems .... 261
§10.1 Classical, integral, and mild solutions ................. 261
§10.2 Semiflow via Lipschitz condition and contraction
principle ............................................... 265
§10.3 Compactness all the way ................................. 266
§10.4 Total trajectories ...................................... 271
§10.5 Positive solutions: The low road ........................ 273
§10.6 Heterogeneous time-autonomous boundary conditions ....... 279
Chapter 11 Microbial Growth in a Tubular Bioreactor ........... 283
§11.1 Model description ....................................... 283
§11.2 The no-bacteria invariant set ........................... 287
§11.3 The solution semiflow ................................... 291
§11.4 Bounds on solutions and the global attractor ............ 292
§11.5 Stability of the washout equilibrium .................... 296
§11.6 Persistence of the microbial population ................. 301
§11.7 Exercises ............................................... 304
Chapter 12 Dividing Cells in a Chemostat ...................... 307
§12.1 An integral equation .................................... 309
§12.2 A C0-semigroup .......................................... 314
§12.3 A semilinear Cauchy problem ............................. 318
§12.4 Extinction and weak persistence via Laplace transform ... 320
§12.5 Exercises ............................................... 325
Chapter 13 Persistence for Nonautonomous Dynamical Systems .... 327
§13.1 The simple chemostat with time-dependent washout rate ... 327
§13.2 General time-heterogeneity .............................. 332
§13.3 Periodic and asymptotically periodic semiflows .......... 335
§13.4 Uniform persistence of the cell population .............. 336
§13.5 Exercises ............................................... 339
Chapter 14 Forced Persistence in Linear Cauchy Problems ....... 341
§14.1 Uniform weak persistence and asymptotic Abel-averages ... 342
§14.2 A compact attracting set ................................ 343
§14.3 Uniform persistence in ordered Banach space ............. 344
Chapter 15 Persistence via Average Lyapunov Functions ......... 349
§15.1 Weak average Lyapunov functions ......................... 350
§15.2 Strong average Lyapunov functions ....................... 354
§15.3 The time-heterogeneous hypercycle equation .............. 355
§15.4 Exercises ............................................... 361
Appendix A Tools from Analysis and Differential Equations ..... 363
§A.l Lower one-sided derivatives .............................. 363
§A.2 Absolutely continuous functions .......................... 364
§A.3 The method of fluctuation ................................ 365
§A.4 Differential inequalities and positivity of solutions .... 367
§A.5 Perron-Frobenius theory .................................. 372
§A.6 Exercises ................................................ 375
Appendix B Tools from Functional Analysis and Integral
Equations ..................................................... 377
§B.l Compact sets in LP( + ....................................................... 97
§4.5 Persistence a la Baron von Munchhausen ................... 99
§4.6 Navigating between alternative persistence functions .... 107
§4.7 A fertility reducing endemic with two stages of
infection ............................................... 110
§4.8 Exercises ............................................... 123
Chapter 5 The Interplay of Attractors, Repellers, and
Persistence ........................................ 125
§5.1 An attractor of points facilitates persistence .......... 125
§5.2 Partition of the global attractor under uniform
persistence ............................................. 127
§5.3 Repellers and dual attractors ........................... 135
§5.4 The cyclic competition model of May and Leonard
revisited ............................................... 139
§5.5 Attractors at the brink of extinction ................... 140
§5.6 An attractor under two persistence functions ............ 141
§5.7 Persistence of bacteria and phages in a chemostat ....... 142
§5.8 Exercises ............................................... 155
Chapter 6 Existence of Nontrivial Fixed Points via
Persistence ........................................ 157
§6.1 Nontrivial fixed points in the global compact
attractor ............................................... 158
§6.2 Periodic solutions of the Lotka-Volterra predator-prey
model ................................................... 160
§6.3 Exercises ............................................... 162
Chapter 7 Nonlinear Matrix Models: Main Act .................. 163
§7.1 Forward invariant balls and compact attractors of
bounded sets ............................................ 163
§7.2 Existence of nontrivial fixed points .................... 165
§7.3 Uniform persistence and persistence attractors .......... 167
§7.4 Stage persistence ....................................... 171
§7.5 Exercises ............................................... 175
Chapter 8 Topological Approaches to Persistence .............. 177
§8.1 Attractors and repellers ................................ 177
§8.2 Chain transitivity and the Butler-McGehee lemma ......... 180
§8.3 Acyclicity implies uniform weak persistence ............. 185
§8.4 Uniform persistence in a food chain ..................... 191
§8.5 The metered endemic model revisited ..................... 196
§8.6 Nonlinear matrix models (epilog): Biennials ............. 199
§8.7 An endemic with vaccination and temporary immunity ...... 209
§8.8 Lyapunov exponents and persistence for ODEs and maps .... 215
§8.9 Exercises ............................................... 229
Chapter 9 An SI Endemic Model with Variable Infectivity ...... 231
§9.1 The model ............................................... 231
§9.2 Host persistence and disease extinction ................. 236
§9.3 Uniform weak disease persistence ........................ 237
§9.4 The semiflow ............................................ 239
§9.5 Existence of a global compact attractor ................. 240
§9.6 Uniform disease persistence ............................. 245
§9.7 Disease extinction and the disease-free equilibrium ..... 247
§9.8 The endemic equilibrium ................................. 249
§9.9 Persistence as a crossroad to global stability .......... 250
§9.10 Measure-valued distributions of infection-age ........... 254
Chapter 10 Semiflows Induced by Semilinear Cauchy Problems .... 261
§10.1 Classical, integral, and mild solutions ................. 261
§10.2 Semiflow via Lipschitz condition and contraction
principle ............................................... 265
§10.3 Compactness all the way ................................. 266
§10.4 Total trajectories ...................................... 271
§10.5 Positive solutions: The low road ........................ 273
§10.6 Heterogeneous time-autonomous boundary conditions ....... 279
Chapter 11 Microbial Growth in a Tubular Bioreactor ........... 283
§11.1 Model description ....................................... 283
§11.2 The no-bacteria invariant set ........................... 287
§11.3 The solution semiflow ................................... 291
§11.4 Bounds on solutions and the global attractor ............ 292
§11.5 Stability of the washout equilibrium .................... 296
§11.6 Persistence of the microbial population ................. 301
§11.7 Exercises ............................................... 304
Chapter 12 Dividing Cells in a Chemostat ...................... 307
§12.1 An integral equation .................................... 309
§12.2 A C0-semigroup .......................................... 314
§12.3 A semilinear Cauchy problem ............................. 318
§12.4 Extinction and weak persistence via Laplace transform ... 320
§12.5 Exercises ............................................... 325
Chapter 13 Persistence for Nonautonomous Dynamical Systems .... 327
§13.1 The simple chemostat with time-dependent washout rate ... 327
§13.2 General time-heterogeneity .............................. 332
§13.3 Periodic and asymptotically periodic semiflows .......... 335
§13.4 Uniform persistence of the cell population .............. 336
§13.5 Exercises ............................................... 339
Chapter 14 Forced Persistence in Linear Cauchy Problems ....... 341
§14.1 Uniform weak persistence and asymptotic Abel-averages ... 342
§14.2 A compact attracting set ................................ 343
§14.3 Uniform persistence in ordered Banach space ............. 344
Chapter 15 Persistence via Average Lyapunov Functions ......... 349
§15.1 Weak average Lyapunov functions ......................... 350
§15.2 Strong average Lyapunov functions ....................... 354
§15.3 The time-heterogeneous hypercycle equation .............. 355
§15.4 Exercises ............................................... 361
Appendix A Tools from Analysis and Differential Equations ..... 363
§A.l Lower one-sided derivatives .............................. 363
§A.2 Absolutely continuous functions .......................... 364
§A.3 The method of fluctuation ................................ 365
§A.4 Differential inequalities and positivity of solutions .... 367
§A.5 Perron-Frobenius theory .................................. 372
§A.6 Exercises ................................................ 375
Appendix B Tools from Functional Analysis and Integral
Equations ..................................................... 377
§B.l Compact sets in LP(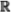 +) ................................... 377
§B.2 Volterra integral equations .............................. 378
§B.3 Fourier transform methods for integro-differential
equations ................................................ 380
§B.4 Closed linear operators .................................. 385
§B.5 Exercises ................................................ 390
Bibliography .................................................. 391
Index ......................................................... 403 +) ................................... 377
§B.2 Volterra integral equations .............................. 378
§B.3 Fourier transform methods for integro-differential
equations ................................................ 380
§B.4 Closed linear operators .................................. 385
§B.5 Exercises ................................................ 390
Bibliography .................................................. 391
Index ......................................................... 403
|