Part I. Introduction to the Geometry of Surfaces and
to Minimal Surfaces
Chapter 1. Differential Geometry of Surfaces in Three-
Dimensional Euclidean Space .......................... 3
1.1 Surfaces in Euclidean Space ................................ 4
1.2 Gauss Map, Weingarten Map. First, Second and Third
Fundamental Form. Mean Curvature and Gauss Curvature ....... 9
1.3 Gauss's Representation Formula, Christoffel Symbols,
Gauss-Codazzi Equations, Theorema Egregium, Minding's
Formula for the Geodesic Curvature ........................ 24
1.4 Conformal Parameters, Gauss-Bonnet Theorem ................ 33
1.5 Covariant Differentiation. The Beltrami Operator .......... 39
1.6 Scholia ................................................... 47
Chapter 2. Minimal Surfaces .................................... 53
2.1 First Variation of Area. Minimal Surfaces ................. 54
2.2 Nonparametric Minimal Surfaces ............................ 58
2.3 Conformal Representation and Analyticity of
Nonparametric Minimal Surfaces ............................ 62
2.4 Bernstein's Theorem ....................................... 66
2.5 Two Characterizations of Minimal Surfaces ................. 72
2.6 Parametric Surfaces in Conformal Parameters. Conformal
Representation of Minimal Surfaces. General Definition
of Minimal Surfaces ....................................... 75
2.7 A Formula for the Mean Curvature .......................... 78
2.8 Absolute and Relative Minima of Area ...................... 82
2.9 Scholia ................................................... 86
Chapter 3. Representation Formulas and Examples of Minimal
Surfaces ............................................ 91
3.1 The Adjoint Surface. Minimal Surfaces as Isotropic
Curves in 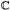 3. Associate Minimal Surfaces .................. 93
3.2 Behavior of Minimal Surfaces Near Branch Points .......... 104
3.3 Representation Formulas for Minimal Surfaces ............. 111
3.4 Björling's Problem. Straight Lines and Planar Lines of
Curvature on Minimal Surfaces. Schwarzian Chains ......... 124
3.5 Examples of Minimal Surfaces ............................. 141
3.5.1 Catenoid and Helicoid ............................. 141
3.5.2 Scherk's Second Surface: The General Minimal
Surface of Helicoidal Type ........................ 146
3.5.3 The Enneper Surface ............................... 151
3.5.4 Bour Surfaces ..................................... 155
3.5.5 Thomsen Surfaces .................................. 156
3.5.6 Scherk's First Surface ............................ 156
3.5.7 The Henneberg Surface ............................. 166
3.5.8 Catalan's Surface ................................. 171
3.5.9 Schwarz's. Surface ................................ 182
3.6 Complete Minimal Surfaces ................................ 183
3.7 Omissions of the Gauss Map of Complete Minimal
Surfaces ................................................. 190
3.8 Scholia .................................................. 200
Color Plates .................................................. 229
Part II. Plateau's Problem
Chapter 4. The Plateau Problem and the Partially Free
Boundary Problem ................................... 239
4.1 Area Functional Versus Dirichlet Integral ................ 246
4.2 Rigorous Formulation of Plateau's Problem and of the
Minimization Process ..................................... 251
4.3 Existence Proof, Part I: Solution of the Variational
Problem .................................................. 255
4.4 The Courant-Lebesgue Lemma ............................... 260
4.5 Existence Proof, Part II: Conformality of Minimizers of
the Dirichlet Integral ................................... 263
4.6 Variant of the Existence Proof. The Partially Free
Boundary Problem ......................................... 275
4.7 Boundary Behavior of Minimal Surfaces with Rectifiable
Boundaries ............................................... 282
4.8 Reflection Principles .................................... 289
4.9 Uniqueness and Nonuniqueness Questions ................... 292
4.10 Another Solution of Plateau's Problem by Minimizing
Area ..................................................... 299
4.11 The Mapping Theorems of Riemann and Lichtenstein ......... 305
4.12 Solution of Plateau's Problem for Nonrectifiable
Boundaries ............................................... 314
4.13 Plateau's Problem for Cartan Functionals ................. 320
4.14 Isoperimetric Inequalities ............................... 327
4.15 Scholia .................................................. 335
Chapter 5. Stable Minimal- and H-Surfaces ..................... 365
5.1 H-Surfaces and Their Normals ............................. 367
5.2 Bonnet's Mapping and Bonnet's Surface .................... 371
5.3 The Second Variation of F for H-Surfaces and Their
Stability ................................................ 376
5.4 On μ-Stable Immersions of Constant Mean Curvature ........ 382
5.5 Curvature Estimates for Stable and Immersed cmc-
Surfaces ................................................. 389
5.6 Nitsche's Uniqueness Theorem and Field-Immersions ........ 395
5.7 Some Finiteness Results for Plateau's Problem ............ 407
5.8 Scholia .................................................. 420
Chapter 6. Unstable Minimal Surfaces .......................... 425
6.1 Courant's Function Ө ..................................... 426
6.2 Courant's Mountain Pass Lemma ............................ 438
6.3 Unstable Minimal Surfaces in a Polygon ................... 442
6.4 The Douglas Functional. Convergence Theorems for
Harmonic Mappings ........................................ 450
6.5 When Is the Limes Superior of a Sequence of Paths Again
a Path? .................................................. 461
6.6 Unstable Minimal Surfaces in Rectifiable Boundaries ...... 463
6.7 Scholia .................................................. 472
6.7.1 Historical Remarks and References to the
Literature ........................................ 472
6.7.2 The Theorem of the Wall for Minimal Surfaces
in Textbooks ...................................... 473
6.7.3 Sources for This Chapter .......................... 474
6.7.4 Multiply Connected Unstable Minimal Surfaces ...... 474
6.7.5 Quasi-Minimal Surfaces ............................ 474
Chapter 7. Graphs with Prescribed Mean Curvature .............. 493
7.1 H-Surfaces with a One-to-One Projection onto a Plane,
and the Nonparametric Dirichlet Problem .................. 494
7.2 Unique Solvability of Plateau's Problem for Contours
with a Nonconvex Projection onto a Plane ................. 508
7.3 Miscellaneous Estimates for Nonparametric H-Surfaces ..... 516
7.4 Scholia .................................................. 529
Chapter 8. Introduction to the Douglas Problem ................ 531
8.1 The Douglas Problem. Examples and Main Result ............ 532
8.2 Conformality of Minimizers of D in e(Г) .................. 538
8.3 Cohesive Sequences of Mappings ........................... 552
8.4 Solution of the Douglas Problem .......................... 561
8.5 Useful Modifications of Surfaces ......................... 563
8.6 Douglas Condition and Douglas Problem .................... 568
8.7 Further Discussion of the Douglas Condition .............. 578
8.8 Examples ................................................. 581
8.9 Scholia .................................................. 584
Problems ...................................................... 587
Appendix 1. On Relative Minimizers of Area and Energy ......... 589
Appendix 2. Minimal Surfaces in Heisenberg Groups ............. 597
Bibliography .................................................. 599
Index ......................................................... 681
|
