Основные обозначения ............................................ 7
Введение ........................................................ 9
Глава I. Основные необходимые сведения из общей теории
устойчивости и теории дихотомий ....................... 16
§ 1. Основные определения устойчивости решений ................. 16
§ 2. Некоторые положения из теории линейных систем ............. 19
2.1. Матрица Коши и ее свойства ........................... 20
2.2. Характеристические показатели решений линейной
системы .............................................. 21
2.3. Устойчивость в линейных системах ..................... 21
2.4. Теорема Перрона о триангуляции линейной системы ...... 22
§ 3. Линейные системы с возмущениями ...................... 22
3.1. Формула Коши для матрицы Коши линейной возмущенной
системы .............................................. 23
3.2. Формула Коши представления решений возмущенной
системы .............................................. 24
3.3. Принцип линейного включения .......................... 25
§ 4. Элементы теории дихотомий ................................. 26
4.1. Прямые суммы подпространств, проекторы и взаимный
наклон подпространств ................................ 26
4.2. Примеры функциональных пространств ................... 27
4.3. Неравенство Гельдера ................................. 28
4.4. Линейные системы с дихотомиями. Основные
определения .......................................... 29
4.5. Функция Грина и ее свойства .......................... 32
4.6. Основная лемма ....................................... 34
4.7. Теорема Коппеля — Конти о роли LP-дихотомии в
задаче об ограниченных решениях линейной
неоднородной системы ................................. 37
Комментарии к главе I ..................................... 39
Глава II. Множества LPS линейных устойчивых систем
Коппеля - Конти ..................................... 42
§ 1. Свойства множества LPS как функции параметра р ............ 42
1.1. Свойство сужаемости множеств LPS при возрастании
параметра р .......................................... 43
1.2. Отсутствие непрерывной зависимости множеств LPS от
параметра р .......................................... 44
1.3. Строгое включение множества ES равномерно
экспоненциально устойчивых систем в предельное
множество 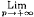 LPS .................................. 48
§ 2. Характеристические показатели решений линейных систем из
множества LPS ............................................. 50
§ 3. Строение внутренности множества LPS ....................... 56
3.1. Открытость множества LPS относительно равномерно
малых возмущений ..................................... 56
3.2. Совпадение внутренности множества LPS относительно
исчезающих на бесконечности возмущений с обычной
внутренностью ........................................ 62
3.3. Экспоненциальная устойчивость нулевого решения
слабо нелинейной системы с линейным приближением
Коппеля — Конти из LPS ............................... 63
§ 4. Строение внутренности предельных множеств LPS .................................. 48
§ 2. Характеристические показатели решений линейных систем из
множества LPS ............................................. 50
§ 3. Строение внутренности множества LPS ....................... 56
3.1. Открытость множества LPS относительно равномерно
малых возмущений ..................................... 56
3.2. Совпадение внутренности множества LPS относительно
исчезающих на бесконечности возмущений с обычной
внутренностью ........................................ 62
3.3. Экспоненциальная устойчивость нулевого решения
слабо нелинейной системы с линейным приближением
Коппеля — Конти из LPS ............................... 63
§ 4. Строение внутренности предельных множеств 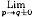 LPS ........ 65
§ 5. О линейных системах с суммируемыми возмущениями ........... 77
5.1. Строение интегральной внутренности множества LPS ..... 77
5.2. Линейные системы с интегрально малыми возмущениями ... 85
5.3. О свойстве включения интегральных внутренностей ...... 87
§ 6. Некоторые обобщения множеств LPS .......................... 89
6.1. Множества L1p(t)S Теоремы о включении и строении
внутренности этих множеств ........................... 90
6.2. Множества L0p(t)S и их свoйства ...................... 102
Комментарии к главе II .............................. 106
Глава III. Множества LPN линейных неустойчивых систем
Коппеля - Конти .................................... 108
§ 1. О свойстве сужаемости множеств LPN при возрастании
параметра р .............................................. 109
§ 2. Оценки снизу характеристических показателей решений
систем из множества LPN .................................. 111
§ 3. Нижние показатели Перрона линейных систем ................ 115
§ 4. О свойстве взаимности множеств Коппеля — Конти ........... 122
§ 5. Линейные системы из множества LPN с равномерно-малыми
и исчезающими на бесконечности линейными возмущениями .... 126
5.1. Строение внутренности множества LPN ................. 126
5.2. Строение внутренности множества LPN относительно
исчезающих на бесконечности возмущений .............. 132
5.3. О неустойчивости нулевого решения слабо нелинейной
системы с линейным приближением из множества LPN .... 135
§ 6. Строение интегральной внутренности множества LPN ......... 136
Комментарии к главе III .................................. 138
Глава IV. Множества LPD линейных систем ...................... 140
§ 1. Критерий LP-дихотомичности линейных систем .............. 140
§ 2. Характеристические показатели решений системы из
множества LPD и их оценки ................................ 143
2.1. Оценки сверху и снизу показателей нетривиальных
решений системы из множества LP D ................... 143
2.2. Угловое сближение взаимно дополнительных
подпространств решений системы из LPD ............... 145
§ 3. Взаимосвязь между различными видами дихотомий ............ 148
§ 4. Влияние возмущений различного вида малости на
свойство LP -дихотомии линейных систем ................... 153
4.1. Свойство открытости множества LPD, р ≥ 1,
линейных систем относительно равномерно малых
возмущений .......................................... 153
4.2. Сохранение свойства LP-дихотомии при суммируемых
возмущениях ......................................... 156
4.3. Ограниченные решения возмущенных линейных
неоднородных систем ................................. 158
§ 5. Слабо нелинейные системы с L1 -дихотомичным
приближением ............................................. 159
Комментарии к главе IV ................................... 163
Глава V. Устойчивость и неустойчивость дифференциальных
систем с линейным приближением Коппеля - Конти ....... 166
§ 1. О неединственности решений системы с возмущениями
высшего порядка малости .................................. 167
§ 2. Экспоненциальная устойчивость дифференциальной системы
с линейным приближением из множества LPS 170
2.1. Критерий совпадения множеств LPS и LPS1
Доказательство достаточности ........................ 171
2.2. Критерий совпадения множеств LPS и LPS1
Доказательство необходимости ........................ 173
2.3. Оценка характеристических показателей решений
возмущенных систем .................................. 179
§ 3. О решениях дифференциальной системы с неустойчивым
линейным приближением из множества LPN ................... 181
3.1. Доказательство достаточности условия р ≥ 1
совпадения множеств LPN1 и LPN ...................... 182
3.2. Доказательство необходимости условия р ≥ 1 для
равенства LPNi = LPN ................................ 184
§ 4. Условная экспоненциальная устойчивость дифференциальной
системы с линейным дихотомичным приближением Коппеля -
Конти .................................................... 198
4.1. Вспомогательное утверждение о равномерной
сходимости последовательности функций ............... 200
4.2. Теорема об условной экспоненциальной устойчивости
нулевого решения возмущенной системы. Построение
множества исчезающих на бесконечности решений ....... 201
4.3. Доказательство отрицательности характеристических
показателей построенных решений ..................... 208
§ 5. Неустойчивость по линейному LP-дихотомичному
приближению .............................................. 215
Комментарии к главе V .................................... 219
Литература .................................................... 221
Именной указатель ............................................. 227
Предметный указатель .......................................... 228
Указатель обозначений ......................................... 230 LPS ........ 65
§ 5. О линейных системах с суммируемыми возмущениями ........... 77
5.1. Строение интегральной внутренности множества LPS ..... 77
5.2. Линейные системы с интегрально малыми возмущениями ... 85
5.3. О свойстве включения интегральных внутренностей ...... 87
§ 6. Некоторые обобщения множеств LPS .......................... 89
6.1. Множества L1p(t)S Теоремы о включении и строении
внутренности этих множеств ........................... 90
6.2. Множества L0p(t)S и их свoйства ...................... 102
Комментарии к главе II .............................. 106
Глава III. Множества LPN линейных неустойчивых систем
Коппеля - Конти .................................... 108
§ 1. О свойстве сужаемости множеств LPN при возрастании
параметра р .............................................. 109
§ 2. Оценки снизу характеристических показателей решений
систем из множества LPN .................................. 111
§ 3. Нижние показатели Перрона линейных систем ................ 115
§ 4. О свойстве взаимности множеств Коппеля — Конти ........... 122
§ 5. Линейные системы из множества LPN с равномерно-малыми
и исчезающими на бесконечности линейными возмущениями .... 126
5.1. Строение внутренности множества LPN ................. 126
5.2. Строение внутренности множества LPN относительно
исчезающих на бесконечности возмущений .............. 132
5.3. О неустойчивости нулевого решения слабо нелинейной
системы с линейным приближением из множества LPN .... 135
§ 6. Строение интегральной внутренности множества LPN ......... 136
Комментарии к главе III .................................. 138
Глава IV. Множества LPD линейных систем ...................... 140
§ 1. Критерий LP-дихотомичности линейных систем .............. 140
§ 2. Характеристические показатели решений системы из
множества LPD и их оценки ................................ 143
2.1. Оценки сверху и снизу показателей нетривиальных
решений системы из множества LP D ................... 143
2.2. Угловое сближение взаимно дополнительных
подпространств решений системы из LPD ............... 145
§ 3. Взаимосвязь между различными видами дихотомий ............ 148
§ 4. Влияние возмущений различного вида малости на
свойство LP -дихотомии линейных систем ................... 153
4.1. Свойство открытости множества LPD, р ≥ 1,
линейных систем относительно равномерно малых
возмущений .......................................... 153
4.2. Сохранение свойства LP-дихотомии при суммируемых
возмущениях ......................................... 156
4.3. Ограниченные решения возмущенных линейных
неоднородных систем ................................. 158
§ 5. Слабо нелинейные системы с L1 -дихотомичным
приближением ............................................. 159
Комментарии к главе IV ................................... 163
Глава V. Устойчивость и неустойчивость дифференциальных
систем с линейным приближением Коппеля - Конти ....... 166
§ 1. О неединственности решений системы с возмущениями
высшего порядка малости .................................. 167
§ 2. Экспоненциальная устойчивость дифференциальной системы
с линейным приближением из множества LPS 170
2.1. Критерий совпадения множеств LPS и LPS1
Доказательство достаточности ........................ 171
2.2. Критерий совпадения множеств LPS и LPS1
Доказательство необходимости ........................ 173
2.3. Оценка характеристических показателей решений
возмущенных систем .................................. 179
§ 3. О решениях дифференциальной системы с неустойчивым
линейным приближением из множества LPN ................... 181
3.1. Доказательство достаточности условия р ≥ 1
совпадения множеств LPN1 и LPN ...................... 182
3.2. Доказательство необходимости условия р ≥ 1 для
равенства LPNi = LPN ................................ 184
§ 4. Условная экспоненциальная устойчивость дифференциальной
системы с линейным дихотомичным приближением Коппеля -
Конти .................................................... 198
4.1. Вспомогательное утверждение о равномерной
сходимости последовательности функций ............... 200
4.2. Теорема об условной экспоненциальной устойчивости
нулевого решения возмущенной системы. Построение
множества исчезающих на бесконечности решений ....... 201
4.3. Доказательство отрицательности характеристических
показателей построенных решений ..................... 208
§ 5. Неустойчивость по линейному LP-дихотомичному
приближению .............................................. 215
Комментарии к главе V .................................... 219
Литература .................................................... 221
Именной указатель ............................................. 227
Предметный указатель .......................................... 228
Указатель обозначений ......................................... 230
|