 | Mazza C. Lecture notes on motivic cohomology / C.Mazza, V.Voevodsky, C.Weibel. - Providence: American Mathematical Society; Cambridge: Clay Mathematics Institute, 2006. - xiv, 216 p.: ill. - (Clay mathematics monographs; Vol.2). - Bibliogr.: p.203-205. - Ind.: p.211-216. - ISBN 0-8218-3847-4; ISBN 978-08218-3847-1; ISSN 1539-6061
|
Preface ....................................................... vii
Introduction ................................................... xi
Part 1. Presheaves with Transfers .............................. 1
Lecture 1. The category of finite correspondences .............. 3
Appendix 1A. The category CorS ...................... 7
Lecture 2. Presheaves with transfers .......................... 13
Homotopy invariant presheaves ...................... 17
Lecture 3. Motivic cohomology ................................. 21
Lecture 4. Weight one motivic cohomology ...................... 25
Lecture 5. Relation to Milnor K-Theory ........................ 29
Part 2. Etale Motivic Theory .................................. 35
Lecture 6. Étale sheaves with transfers ....................... 37
Lecture 7. The relative Picard group and Suslin's Rigidity
Theorem ............................................ 47
Lecture 8. Derived tensor products ............................ 55
Appendix 8A. Tensor triangulated categories ........ 63
Lecture 9. 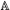 1-weak equivalence ................................ 67
Étale 1-weak equivalence ................................ 67
Étale 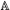 1 -local complexes .......................... 71
Lecture 10. Étale motivic cohomology and algebraic singular
homology ........................................... 75
Part 3. Nisnevich Sheaves with Transfers ...................... 81
Lecture 11. Standard triples ................................... 83
Lecture 12. Nisnevich sheaves .................................. 89
The cdh topology ................................... 94
Lecture 13. Nisnevich sheaves with transfers ................... 99
Cdh sheaves with transfers ........................ 105
Part 4. The Triangulated Category of Motives ................. 107
Lecture 14. The category of motives ........................... 109
Nisnevich 1 -local complexes .......................... 71
Lecture 10. Étale motivic cohomology and algebraic singular
homology ........................................... 75
Part 3. Nisnevich Sheaves with Transfers ...................... 81
Lecture 11. Standard triples ................................... 83
Lecture 12. Nisnevich sheaves .................................. 89
The cdh topology ................................... 94
Lecture 13. Nisnevich sheaves with transfers ................... 99
Cdh sheaves with transfers ........................ 105
Part 4. The Triangulated Category of Motives ................. 107
Lecture 14. The category of motives ........................... 109
Nisnevich 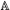 1 -local complexes ..................... 111
Motives with 1 -local complexes ..................... 111
Motives with 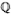 -coefficients ....................... 116
Lecture 15. The complex -coefficients ....................... 116
Lecture 15. The complex 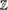 (n) and (n) and 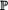 n ........................... 119
Lecture 16. Equidimensional cycles ............................ 125
Motives with compact support ...................... 128
Part 5. Higher Chow Groups ................................... 133
Lecture 17. Higher Ghow groups ................................ 135
Appendix 17A. Cycle maps .......................... 143
Lecture 18. Higher Chow groups and equidimensional cycles ..... 149
Appendix 18A. Generic equidimensionality .......... 155
Lecture 19. Motivic cohomology and higher Chow groups ......... 159
Lecture 20. Geometric motives ................................. 167
Part 6. Zariski Sheaves with Transfers ....................... 173
Lecture 21. Covering morphisms of triples ..................... 175
Lecture 22. Zariski sheaves with transfers .................... 183
Lecture 23. Contractions ...................................... 191
Lecture 24. Homotopy invariance of cohomology ................. 197
Bibliography .................................................. 203
Glossary ...................................................... 207
Index ......................................................... 211 n ........................... 119
Lecture 16. Equidimensional cycles ............................ 125
Motives with compact support ...................... 128
Part 5. Higher Chow Groups ................................... 133
Lecture 17. Higher Ghow groups ................................ 135
Appendix 17A. Cycle maps .......................... 143
Lecture 18. Higher Chow groups and equidimensional cycles ..... 149
Appendix 18A. Generic equidimensionality .......... 155
Lecture 19. Motivic cohomology and higher Chow groups ......... 159
Lecture 20. Geometric motives ................................. 167
Part 6. Zariski Sheaves with Transfers ....................... 173
Lecture 21. Covering morphisms of triples ..................... 175
Lecture 22. Zariski sheaves with transfers .................... 183
Lecture 23. Contractions ...................................... 191
Lecture 24. Homotopy invariance of cohomology ................. 197
Bibliography .................................................. 203
Glossary ...................................................... 207
Index ......................................................... 211
|
|