 | Dehornoy P. Ordering braids / P.Dehornoy; with I.Dynnikov, D.Rolfsen, B.Wiest. - Providence: American Mathematical Society, 2008. - ix, 323 p.: ill. - (Mathematical surveys and monographs; Vol.148). - ix, 323 p.: ill. - Bibliogr.: p.311-317. - Ind.: p.319-323. - ISBN 978-0-8218-4431-1; ISSN 0076-5376
|
Preface ........................................................ ix
Introduction .................................................... 1
A meeting of two classical subjects .......................... 1
A convergence of approaches .................................. 3
Organization of the text ..................................... 5
Guidelines to the reader ..................................... 7
Acknowledgements ............................................. 8
Chapter I. Braid Groups ....................................... 9
1. The Artin presentation ....................................... 9
2. Isotopy classes of braid diagrams ........................... 10
3. Mapping class groups ........................................ 12
4. Positive braids ............................................. 14
Chapter II. A Linear Ordering of Braids ....................... 19
1. The σ-ordering of Bn ........................................ 19
2. Local properties of the σ-ordering .......................... 26
3. Global properties of the σ-ordering ......................... 29
4. The σ-ordering of positive braids ........................... 35
Chapter III. Applications of the Braid Ordering ................ 43
1. Consequences of orderability ................................ 44
2. Applications of more specific properties .................... 46
3. Application of well-orderability ............................ 50
Chapter IV. Self-distributivity ............................... 55
1. Colouring positive braids ................................... 56
2. Colouring arbitrary braids .................................. 66
3. The group of left self-distributivity ....................... 76
4. Normal forms in free LD-systems ............................. 81
5. Appendix: Iterations of elementary embeddings in set
theory ...................................................... 84
Chapter V. Handle Reduction .................................. 87
1. Description of handle reduction ............................. 87
2. Convergence of handle reduction ............................. 92
3. Special cases and variants ................................. 102
Chapter VI. Connection with the Garside Structure ............ 107
1. The degree of a positive braid ............................. 108
2. Proving Property С using a counting argument ............... 113
3. The increasing enumeration of Div(Δdn) ..................... 117
Chapter VII. Alternating Decompositions ....................... 129
1. The Φn-splitting of a braid in B+n ......................... 130
2. The Φ-normal form .......................................... 135
3. Burckel's approach ......................................... 143
4. Applications ............................................... 148
Chapter VIII.Dual Braid Monoids ............................... 153
1. Dual braid monoids ......................................... 154
2. The 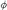 -normal form on Bn+* ................................... 159
3. Connection between orders .................................. 163
Chapter IX. Automorphisms of a Free Group .................... 173
1. Artin representation of σ-positive braids .................. 173
2. Prom an automorphism back to a braid ....................... 178
3. Pulling back orderings of free groups ...................... 182
Chapter X. Curve Diagrams ................................... 185
1. A braid ordering using curve diagrams ...................... 185
2. Proof of Properties A, C, and S ............................ 189
Chapter XI Relaxation Algorithms ............................ 195
1. Bressaud's regular language of relaxation braids ........... 196
2. The transmission-relaxation normal form of braids .......... 204
Chapter XII. Triangulations ................................... 221
1. The coordinates of a braid ................................. 222
2. Triangulations and laminations ............................. 225
3. The Mosher normal form ..................................... 236
Chapter XIII.Hyperbolic Geometry .............................. 247
1. Uncountably many orderings of the braid group .............. 248
2. The classification of orderings induced by the action on -normal form on Bn+* ................................... 159
3. Connection between orders .................................. 163
Chapter IX. Automorphisms of a Free Group .................... 173
1. Artin representation of σ-positive braids .................. 173
2. Prom an automorphism back to a braid ....................... 178
3. Pulling back orderings of free groups ...................... 182
Chapter X. Curve Diagrams ................................... 185
1. A braid ordering using curve diagrams ...................... 185
2. Proof of Properties A, C, and S ............................ 189
Chapter XI Relaxation Algorithms ............................ 195
1. Bressaud's regular language of relaxation braids ........... 196
2. The transmission-relaxation normal form of braids .......... 204
Chapter XII. Triangulations ................................... 221
1. The coordinates of a braid ................................. 222
2. Triangulations and laminations ............................. 225
3. The Mosher normal form ..................................... 236
Chapter XIII.Hyperbolic Geometry .............................. 247
1. Uncountably many orderings of the braid group .............. 248
2. The classification of orderings induced by the action on
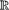 .......................................................... 256
3. The subword property for all Nielsen-Thurston type
orderings .................................................. 263
Chapter XIV. The Space of all Braid Orderings ................. 265
1. The spaces of orderings on a group ......................... 265
2. The space of left-orderings of the braid groups ............ 268
Chapter XV. Bi-ordering the Pure Braid Groups ................ 273
1. Lower central series ....................................... 273
2. Artin coordinates and Magnus expansion ..................... 274
3. The Magnus ordering of PBn ................................. 279
4. The ordering of positive pure braids ....................... 283
5. Incompatibility of the orderings ........................... 286
Chapter XVI. Open Questions and Extensions .................... 291
1. General questions .......................................... 291
2. More specific questions .................................... 293
3. Generalizations and extensions.............................. 301
Key Definitions ............................................... 309
Bibliography .................................................. 311
Index of Notation ............................................. 319
Index ......................................................... 321 .......................................................... 256
3. The subword property for all Nielsen-Thurston type
orderings .................................................. 263
Chapter XIV. The Space of all Braid Orderings ................. 265
1. The spaces of orderings on a group ......................... 265
2. The space of left-orderings of the braid groups ............ 268
Chapter XV. Bi-ordering the Pure Braid Groups ................ 273
1. Lower central series ....................................... 273
2. Artin coordinates and Magnus expansion ..................... 274
3. The Magnus ordering of PBn ................................. 279
4. The ordering of positive pure braids ....................... 283
5. Incompatibility of the orderings ........................... 286
Chapter XVI. Open Questions and Extensions .................... 291
1. General questions .......................................... 291
2. More specific questions .................................... 293
3. Generalizations and extensions.............................. 301
Key Definitions ............................................... 309
Bibliography .................................................. 311
Index of Notation ............................................. 319
Index ......................................................... 321
|
|