Introduction .................................................. vii
Part 1. Quasiminimal Excellence and Complex Exponentiation ..... 1
Chapter 1. Combinatorial Geometries and Infinitary Logics ...... 3
1.1. Combinatorial Geometries ............................... 3
1.2. Infinitary Logic ....................................... 4
Chapter 2. Abstract Quasiminimality ............................ 7
Chapter 3. Covers of the Multiplicative Group of 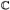 ............ 17
Part 2. Abstract Elementary Classes ........................... 25
Chapter 4. Abstract Elementary Classes ........................ 27
Chapter 5. Two Basic Results about Lωl,ω(Q) .................... 39
5.1. Non-definability of Well-order in Lωl,ω(Q) ............. 39
5.2. The Number of Models in ω1 ............................ 41
Chapter 6. Categoricity Implies Completeness .................. 45
6.1. Completeness .......................................... 45
6.2. Arbitrarily Large Models .............................. 50
6.3. Few Models in Small Cardinals ......................... 52
6.4. Categoricity and Completeness for Lωl,ω(Q) ............. 54
Chapter 7. A Model in ............ 17
Part 2. Abstract Elementary Classes ........................... 25
Chapter 4. Abstract Elementary Classes ........................ 27
Chapter 5. Two Basic Results about Lωl,ω(Q) .................... 39
5.1. Non-definability of Well-order in Lωl,ω(Q) ............. 39
5.2. The Number of Models in ω1 ............................ 41
Chapter 6. Categoricity Implies Completeness .................. 45
6.1. Completeness .......................................... 45
6.2. Arbitrarily Large Models .............................. 50
6.3. Few Models in Small Cardinals ......................... 52
6.4. Categoricity and Completeness for Lωl,ω(Q) ............. 54
Chapter 7. A Model in 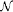 2 ...................................... 57
Part 3. Abstract Elementary Classes with Arbitrarily Large
Models ................................................ 63
Chapter 8. Galois types, Saturation, and Stability ............ 67
Chapter 9. Brimful Models ..................................... 73
Chapter 10. Special, Limit and Saturated Models ................ 75
Chapter 11. Locality and Tameness............................... 83
Chapter 12. Splitting and Minimality ........................... 91
Chapter 13. Upward Categoricity Transfer ....................... 99
Chapter 14. Omitting Types and Downward Categoricity .......... 105
Chapter 15. Unions of Saturated Models ........................ 113
Chapter 16. Life without Amalgamation ......................... 119
Chapter 17. Amalgamation and Few Models ....................... 125
Part 4. Categoricity in Lωl,ω ................................. 133
Chapter 18. Atomic AEC ........................................ 137
Chapter 19. Independence in ω-stable Classes .................. 143
Chapter 20. Good Systems ...................................... 151
Chapter 21. Excellence Goes Up ................................ 159
Chapter 22. Very Few Models Implies Excellence ................ 165
Chapter 23. Very Few Models Implies Amalgamation over Pairs ... 173
Chapter 24. Excellence and *-Excellence ....................... 179
Chapter 25. Quasiminimal Sets and Categoricity Transfer ....... 185
Chapter 26. Demystifying Non-excellence ....................... 193
26.1. The Basic Structure .................................. 193
26.2. Solutions and Categoricity ........................... 196
26.3. Disjoint Amalgamation for Models of 2 ...................................... 57
Part 3. Abstract Elementary Classes with Arbitrarily Large
Models ................................................ 63
Chapter 8. Galois types, Saturation, and Stability ............ 67
Chapter 9. Brimful Models ..................................... 73
Chapter 10. Special, Limit and Saturated Models ................ 75
Chapter 11. Locality and Tameness............................... 83
Chapter 12. Splitting and Minimality ........................... 91
Chapter 13. Upward Categoricity Transfer ....................... 99
Chapter 14. Omitting Types and Downward Categoricity .......... 105
Chapter 15. Unions of Saturated Models ........................ 113
Chapter 16. Life without Amalgamation ......................... 119
Chapter 17. Amalgamation and Few Models ....................... 125
Part 4. Categoricity in Lωl,ω ................................. 133
Chapter 18. Atomic AEC ........................................ 137
Chapter 19. Independence in ω-stable Classes .................. 143
Chapter 20. Good Systems ...................................... 151
Chapter 21. Excellence Goes Up ................................ 159
Chapter 22. Very Few Models Implies Excellence ................ 165
Chapter 23. Very Few Models Implies Amalgamation over Pairs ... 173
Chapter 24. Excellence and *-Excellence ....................... 179
Chapter 25. Quasiminimal Sets and Categoricity Transfer ....... 185
Chapter 26. Demystifying Non-excellence ....................... 193
26.1. The Basic Structure .................................. 193
26.2. Solutions and Categoricity ........................... 196
26.3. Disjoint Amalgamation for Models of 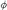 k ............... 200
26.4. Tameness ............................................. 201
26.5. Instability and Non-tameness ......................... 202
Appendix A. Morley's Omitting Types Theorem ................... 205
Appendix B. Omitting Types in Uncountable Models .............. 211
Appendix C. Weak Diamonds ..................................... 217
Appendix D. Problems .......................................... 223
Bibliography .................................................. 227
Index ......................................................... 233 k ............... 200
26.4. Tameness ............................................. 201
26.5. Instability and Non-tameness ......................... 202
Appendix A. Morley's Omitting Types Theorem ................... 205
Appendix B. Omitting Types in Uncountable Models .............. 211
Appendix C. Weak Diamonds ..................................... 217
Appendix D. Problems .......................................... 223
Bibliography .................................................. 227
Index ......................................................... 233
|