Preface ...................................................... xiii
Introduction .................................................... 1
Armand Borel, Automorphic Forms on Reductive Groups ............. 5
Introduction .................................................... 7
1. Notation .................................................... 7
2. Notion of automorphic form .................................. 8
3. First properties of automorphic forms ....................... 9
4. Reductive groups (review) .................................. 12
5. Arithmetic subgroups. Reduction theory ..................... 19
6. Constant terms. The basic estimate ......................... 24
7. Finite dimensionality of А(Г, J, ξ) ........................ 28
8. Convolution operators on cuspidal functions ................ 29
9. Automorphic forms and the regular representation on Г\G .... 30
10. A decomposition of the space of automorphic forms .......... 32
11. Some estimates of growth functions ......................... 33
12. Eisenstein series .......................................... 35
Bibliography ................................................... 39
L. Clozel, Spectral Theory of Automorphic Forms ................ 41
Foreword ....................................................... 43
Lecture 1. Mostly SL(2) ........................................ 47
Lecture 2. The spectral decomposition of L2(G(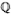 )\G( )\G(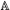 )):
Arthur's conjectures ................................ 57
Lecture 3. Known bounds for the cuspidal spectrum and
the Burger-Sarnak method ............................ 65
Lecture 4. Applications: control of the spectrum ............... 79
Appendix: All reductive adelic groups are tame ................. 87
Bibliography ................................................... 89
James W. Cogdell, L-functions and Converse Theorems for GLn .... 95
Introduction ................................................... 97
Lecture 1. Fourier expansions and multiplicity one ............ 101
Lecture 2. Eulerian integrals for GLn ......................... 111
Lecture 3. Local L-functions .................................. 123
Lecture 4. Global L-functions ................................. 137
Lecture 5. Converse theorems .................................. 147
Lecture 6. Converse theorems and functoriality ................ 161
Bibliography .................................................. 173
Philippe Michel, Analytic Number Theory and Families of
Automorphic L-functions ....................................... 179
Foreword ...................................................... 181
Lecture 1. Analytic properties of individual L-functions ...... 187
Lecture 2. A review of classical automorphic forms ............ 211
Lecture 3. Large sieve inequalities ........................... 223
Lecture 4. The subconvexity problem ........................... 241
Lecture 5. Some applications of subconvexity .................. 267
Bibliography .................................................. 285
Freydoon Shahidi, Langlands-Shahidi Method .................... 297
Foreword ...................................................... 299
Lecture 1. Basic concepts ..................................... 301
Lecture 2. Eisenstein series and L-functions .................. 307
Lecture 3. Functional equations and multiplicativity .......... 315
Lecture 4. Holomorphy and boundedness; applications ........... 321
Bibliography .................................................. 327
Audrey Terras, Arithmetical Quantum Chaos ..................... 331
Abstract ...................................................... 333
Lecture 1. Finite models ...................................... 335
Lecture 2. Three symmetric spaces ............................. 355
Bibliography .................................................. 371
David A. Vogan, Jr, Isolated Unitary Representations .......... 377
Bibliography .................................................. 397
Wen-Ching Winnie Li, Ramanujan Graphs and Ramanujan
Hypergraphs ................................................... 399
Introduction .................................................. 401
Lecture 1. Ramanujan graphs and connections with number
theory ............................................. 403
Lecture 2. Ramanujan hypergraphs .............................. 415
Bibliography .................................................. 425 )):
Arthur's conjectures ................................ 57
Lecture 3. Known bounds for the cuspidal spectrum and
the Burger-Sarnak method ............................ 65
Lecture 4. Applications: control of the spectrum ............... 79
Appendix: All reductive adelic groups are tame ................. 87
Bibliography ................................................... 89
James W. Cogdell, L-functions and Converse Theorems for GLn .... 95
Introduction ................................................... 97
Lecture 1. Fourier expansions and multiplicity one ............ 101
Lecture 2. Eulerian integrals for GLn ......................... 111
Lecture 3. Local L-functions .................................. 123
Lecture 4. Global L-functions ................................. 137
Lecture 5. Converse theorems .................................. 147
Lecture 6. Converse theorems and functoriality ................ 161
Bibliography .................................................. 173
Philippe Michel, Analytic Number Theory and Families of
Automorphic L-functions ....................................... 179
Foreword ...................................................... 181
Lecture 1. Analytic properties of individual L-functions ...... 187
Lecture 2. A review of classical automorphic forms ............ 211
Lecture 3. Large sieve inequalities ........................... 223
Lecture 4. The subconvexity problem ........................... 241
Lecture 5. Some applications of subconvexity .................. 267
Bibliography .................................................. 285
Freydoon Shahidi, Langlands-Shahidi Method .................... 297
Foreword ...................................................... 299
Lecture 1. Basic concepts ..................................... 301
Lecture 2. Eisenstein series and L-functions .................. 307
Lecture 3. Functional equations and multiplicativity .......... 315
Lecture 4. Holomorphy and boundedness; applications ........... 321
Bibliography .................................................. 327
Audrey Terras, Arithmetical Quantum Chaos ..................... 331
Abstract ...................................................... 333
Lecture 1. Finite models ...................................... 335
Lecture 2. Three symmetric spaces ............................. 355
Bibliography .................................................. 371
David A. Vogan, Jr, Isolated Unitary Representations .......... 377
Bibliography .................................................. 397
Wen-Ching Winnie Li, Ramanujan Graphs and Ramanujan
Hypergraphs ................................................... 399
Introduction .................................................. 401
Lecture 1. Ramanujan graphs and connections with number
theory ............................................. 403
Lecture 2. Ramanujan hypergraphs .............................. 415
Bibliography .................................................. 425
|