Introduction .................................................... 1
0.1. Noncommutative function spaces ............................. 2
0.2. Amalgamated Lp spaces ...................................... 3
0.3. Conditional Lp spaces ...................................... 5
0.4. Intersection spaces ........................................ 7
0.5. Mixed-norm inequalities .................................... 8
0.6. Operator space Lp embeddings ............................... 9
Chapter 1. Noncommutative integration .......................... 13
1.1. Noncommutative Lp spaces .................................. 13
1.2. Pisier's vector-valued Lp spaces .......................... 17
1.3. The spaces Lpr(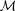 , E) and Lpc( , E) and Lpc(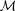 , E) ...................... 20
Chapter 2. Amalgamated Lp spaces ............................... 27
2.1. Haagerup's construction ................................... 29
2.2. Triangle inequality on ∂∞ K ............................... 31
2.3. A metric structure on the solid К ......................... 38
Chapter 3. An interpolation theorem ............................ 43
3.1. Finite von Neumann algebras ............................... 44
3.2. Conditional expectations on ∂∞ K .......................... 48
3.3. General von Neumann algebras I ............................ 55
3.4. General von Neumann algebras II ........................... 61
3.5. Proof of the main interpolation theorem ................... 66
Chapter 4. Conditional Lp spaces ............................... 71
4.1. Duality ................................................... 72
4.2. Conditional L∞ spaces ..................................... 73
4.3. Interpolation results and applications .................... 74
Chapter 5. Intersections of Lp spaces .......................... 79
5.1. Free Rosenthal inequalities ............................... 79
5.2. Estimates for BMO type norms .............................. 83
5.3. Interpolation of 2-term intersections ..................... 99
5.4. Interpolation of 4-term intersections .................... 103
Chapter 6. Factorization of , E) ...................... 20
Chapter 2. Amalgamated Lp spaces ............................... 27
2.1. Haagerup's construction ................................... 29
2.2. Triangle inequality on ∂∞ K ............................... 31
2.3. A metric structure on the solid К ......................... 38
Chapter 3. An interpolation theorem ............................ 43
3.1. Finite von Neumann algebras ............................... 44
3.2. Conditional expectations on ∂∞ K .......................... 48
3.3. General von Neumann algebras I ............................ 55
3.4. General von Neumann algebras II ........................... 61
3.5. Proof of the main interpolation theorem ................... 66
Chapter 4. Conditional Lp spaces ............................... 71
4.1. Duality ................................................... 72
4.2. Conditional L∞ spaces ..................................... 73
4.3. Interpolation results and applications .................... 74
Chapter 5. Intersections of Lp spaces .......................... 79
5.1. Free Rosenthal inequalities ............................... 79
5.2. Estimates for BMO type norms .............................. 83
5.3. Interpolation of 2-term intersections ..................... 99
5.4. Interpolation of 4-term intersections .................... 103
Chapter 6. Factorization of 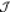 np,q( np,q(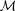 , E) ...................... 107
6.1. Amalgamated tensors ...................................... 108
6.2. Conditional expectations and ultraproducts ............... 112
6.3. Factorization of the space , E) ...................... 107
6.1. Amalgamated tensors ...................................... 108
6.2. Conditional expectations and ultraproducts ............... 112
6.3. Factorization of the space 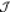 n∞,1( n∞,1(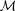 , E) ................. 115
Chapter 7. Mixed-norm inequalities ........................... 119
7.1. Embedding of , E) ................. 115
Chapter 7. Mixed-norm inequalities ........................... 119
7.1. Embedding of 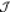 np,q( np,q(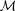 , E) into Lp( , E) into Lp( ; ℓqn) ............... 119
7.2. Asymmetric Lp spaces and noncommutative (∑pq) ............ 126
Chapter 8. Operator space Lp embeddings ....................... 129
8.1. Embedding Schatten classes ............................... 129
8.2. Embedding into the hyperfinite factor .................... 132
8.3. Embedding for general von Neumann algebras ............... 144
8.1. Bibliography ............................................. 153 ; ℓqn) ............... 119
7.2. Asymmetric Lp spaces and noncommutative (∑pq) ............ 126
Chapter 8. Operator space Lp embeddings ....................... 129
8.1. Embedding Schatten classes ............................... 129
8.2. Embedding into the hyperfinite factor .................... 132
8.3. Embedding for general von Neumann algebras ............... 144
8.1. Bibliography ............................................. 153
|