I Lorentz geometry ............................................. 1
1 Introduction ................................................. 1
2 Manifolds .................................................... 1
3 Differentiable mappings ...................................... 2
4 Vectors and tensors .......................................... 2
4.1 Tangent and cotangent space ............................. 2
4.2 Vector fields ........................................... 3
4.3 Tensors and tensor fields ............................... 5
5 Pseudo-Riemannian metrics .................................... 6
5.1 General properties ...................................... 6
5.2 Riemannian and Lorentzian metrics ....................... 8
6 Riemannian connection ........................................ 9
7 Geodesies ................................................... 12
8 Curvature ................................................... 13
9 Geodesic deviation .......................................... 14
10 Maximum of length and conjugate points ...................... 15
11 Linearized Ricci and Einstein tensors ....................... 17
12 Second derivative of the Ricci tensor ....................... 17
II Special Relativity ......................................... 19
1 Newton's mechanics .......................................... 19
1.1 The Galileo-Newton spacetime ........................... 19
1.2 Newton's dynamics - the Galileo group .................. 20
2 Maxwell's equations ......................................... 20
3 Minkowski spacetime ......................................... 21
3.1 Definition ............................................. 21
3.2 Maxwell's equations on M4 .............................. 22
4 Poincaré group .............................................. 23
5 Lorentz group ............................................... 24
5.1 General formulae ....................................... 24
5.2 Transformation of electric and magnetic vector fields
(case n = 3) ........................................... 25
5.3 Lorentz contraction and dilatation ..................... 26
6 Special Relativity .......................................... 26
6.1 Proper time ............................................ 26
6.2 Proper frame and relative velocities ................... 28
7 Dynamics of a pointlike mass ................................ 30
7.1 Newtonian law .......................................... 30
7.2 Relativistic law ....................................... 30
7.3 Equivalence of mass and energy ......................... 32
8 Continuous matter ........................................... 33
8.1 Case of dust (incoherent matter) ....................... 34
8.2 Perfect fluids ......................................... 35
III General relativity and Einstein's equations ............... 37
1 Introduction ................................................ 37
2 Newton's gravity law ........................................ 37
3 General relativity .......................................... 39
3.1 Physical motivations ................................... 39
4 Observations and experiments ................................ 40
4.1 Deviation of light rays ................................ 40
4.2 Proper time, gravitational time delay .................. 40
5 Einstein's equations ........................................ 42
5.1 Vacuum case ............................................ 42
5.2 Equations with sources ................................. 43
6 Field sources ............................................... 45
6.1 Electromagnetic sources ................................ 45
6.2 Electromagnetic potential .............................. 47
6.3 Yang-Mills fields ...................................... 47
6.4 Scalar fields .......................................... 49
6.5 Wave maps .............................................. 49
6.6 Energy conditions ...................................... 51
7 Lagrangians ................................................. 51
7.1 Einstein-Hilbert Lagrangian ............................ 51
7.2 Lagrangians and stress energy tensors of sources ....... 52
7.3 Coupled Lagrangian ..................................... 53
8 Fluid sources ............................................... 54
9 Einsteinian spacetimes ...................................... 55
9.1 Definition ............................................. 55
9.2 Regularity hypotheses .................................. 55
10 Newtonian approximation ..................................... 57
10.1 Equations for potentials ............................... 57
10.2 Equations of motion .................................... 59
11 Gravitational waves ......................................... 60
11.1 Minkowskian approximation .............................. 60
11.2 General linear waves ................................... 61
12 High-frequency gravitational waves .......................... 62
12.1 Phase and polarizations ................................ 64
12.2 Radiative coordinates .................................. 66
12.3 Energy conservation .................................... 68
13 Coupled electromagnetic and gravitational waves ............. 68
13.1 Phase and polarizations ................................ 69
13.2 Propagation equations .................................. 69
IV Schwarzschild spacetime and black holes .................... 72
1 Introduction ................................................ 72
2 Spherically symmetric spacetimes ............................ 72
3 Schwarzschild metric ........................................ 74
4 Other coordinates ........................................... 75
4.1 Isotropic coordinates .................................. 75
4.2 Wave coordinates ....................................... 76
4.3 Painlevé-Gullstrand-like coordinates ................... 77
4.4 Regge-Wheeler coordinates .............................. 77
5 Schwarzschild spacetime ..................................... 78
6 The motion of the planets and perihelion precession ......... 78
6.1 Equations .............................................. 78
6.2 Results of observations ................................ 81
6.3 Escape velocity ........................................ 81
7 Stability of circular orbits ................................ 83
8 Deflection of light rays .................................... 84
8.1 Theoretical prediction ................................. 84
8.2 Results of observation ................................. 85
8.3 Fermat's principle and light travel parameter time ..... 85
9 Red shift and time delay .................................... 86
10 Spherically symmetric interior solutions .................... 87
10.1 Static solutions. Upper limit on mass .................. 88
10.2 Matching with an exterior solution ..................... 91
10.3 Non-static solutions ................................... 91
11 The Schwarzschild black hole ................................ 92
11.1 The event horizon ...................................... 92
11.2 The Eddington-Finkelstein extension .................... 93
11.3 Eddington-Finkelstein white hole ....................... 94
11.4 Kruskal complete spacetime ............................. 94
11.5 Observations ........................................... 96
12 Spherically symmetric gravitational collapse ............... 96
12.1 Tolman metric .......................................... 98
12.2 Monotonically decreasing density ...................... 101
13 The Reissner-Nordstrom solution ............................ 103
14 Schwarzschild spacetime in dimension n + 1 ................. 104
14.1 Standard coordinates .................................. 104
14.2 Wave coordinates ...................................... 104
V Cosmology ................................................... 106
1 Introduction ............................................... 106
2 Cosmological principle ..................................... 107
3 Isotropic and homogeneous Riemannian manifolds ............. 108
3.1 Isotropy .............................................. 108
3.2 Homogeneity ........................................... 109
4 Robertson-Walker spacetimes ................................ 111
4.1 Space metrics ......................................... 112
4.2 Robertson-Walker spacetime metrics .................... 113
4.3 Robertson-Walker dynamics ............................. 113
4.4 Einstein static universe .............................. 115
4.5 Cosmological red shift and the Hubble constant ........ 115
4.6 De Sitter spacetime ................................... 118
4.7 Anti de Sitter (AdS) spacetime ........................ 120
5 Friedmann-Lema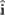 tre models .................................. 121
5.1 Equation of state ..................................... 121
5.2 General properties .................................... 122
5.3 Priedmann models ...................................... 123
5.4 Some other models ..................................... 124
5.5 Confrontation with observations ....................... 125
6 Homogeneous non-isotropic cosmologies ...................... 125
7 Bianchi class I universes .................................. 128
7.1 Kasner solutions ...................................... 128
7.2 Models with matter .................................... 131
8 Bianchi type IX ............................................ 132
9 The Kantowski-Sachs models ................................. 134
10 Taub and Taub NUT spacetimes ............................... 135
10.1 Taub spacetime ........................................ 135
10.2 Taub NUT spacetime .................................... 136
11 Locally homogeneous models ................................. 136
11.1 n-dimensional compact manifolds ....................... 137
11.2 Compact 3-manifolds ................................... 139
12 Recent observations and conjectures ........................ 140
VI Local Cauchy problem ....................................... 142
1 Introduction ............................................... 142
2 Moving frame formulae ...................................... 142
2.1 Frame and coframe ..................................... 142
2.2 Metric ................................................ 143
2.3 Connection ............................................ 144
2.4 Curvature ............................................. 145
3 n + 1 splitting adapted to space slices .................... 146
3.1 Adapted frame and coframe ............................. 146
3.2 Structure coefficients ................................ 147
3.3 Splitting of the connection ........................... 147
3.4 Extrinsic curvature ................................... 148
3.5 Splitting of the Riemann tensor ....................... 148
4 Constraints and evolution .................................. 149
4.1 Equations. Conservation of constraints ................ 149
5 Hamiltonian and symplectic formulation ..................... 151
5.1 Hamilton equations .................................... 151
5.2 Symplectic formulation ................................ 154
6 Cauchy problem ............................................. 155
6.1 Definitions ........................................... 155
6.2 The analytic case ..................................... 156
7 Wave gauges ................................................ 157
7.1 Wave coordinates ...................................... 158
7.2 Generalized wave coordinates .......................... 161
7.3 Damped wave coordinates ............................... 162
7.4 Globalization in space, tre models .................................. 121
5.1 Equation of state ..................................... 121
5.2 General properties .................................... 122
5.3 Priedmann models ...................................... 123
5.4 Some other models ..................................... 124
5.5 Confrontation with observations ....................... 125
6 Homogeneous non-isotropic cosmologies ...................... 125
7 Bianchi class I universes .................................. 128
7.1 Kasner solutions ...................................... 128
7.2 Models with matter .................................... 131
8 Bianchi type IX ............................................ 132
9 The Kantowski-Sachs models ................................. 134
10 Taub and Taub NUT spacetimes ............................... 135
10.1 Taub spacetime ........................................ 135
10.2 Taub NUT spacetime .................................... 136
11 Locally homogeneous models ................................. 136
11.1 n-dimensional compact manifolds ....................... 137
11.2 Compact 3-manifolds ................................... 139
12 Recent observations and conjectures ........................ 140
VI Local Cauchy problem ....................................... 142
1 Introduction ............................................... 142
2 Moving frame formulae ...................................... 142
2.1 Frame and coframe ..................................... 142
2.2 Metric ................................................ 143
2.3 Connection ............................................ 144
2.4 Curvature ............................................. 145
3 n + 1 splitting adapted to space slices .................... 146
3.1 Adapted frame and coframe ............................. 146
3.2 Structure coefficients ................................ 147
3.3 Splitting of the connection ........................... 147
3.4 Extrinsic curvature ................................... 148
3.5 Splitting of the Riemann tensor ....................... 148
4 Constraints and evolution .................................. 149
4.1 Equations. Conservation of constraints ................ 149
5 Hamiltonian and symplectic formulation ..................... 151
5.1 Hamilton equations .................................... 151
5.2 Symplectic formulation ................................ 154
6 Cauchy problem ............................................. 155
6.1 Definitions ........................................... 155
6.2 The analytic case ..................................... 156
7 Wave gauges ................................................ 157
7.1 Wave coordinates ...................................... 158
7.2 Generalized wave coordinates .......................... 161
7.3 Damped wave coordinates ............................... 162
7.4 Globalization in space, 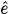 wave gauges ................. 162
7.5 Local in time existence in a wave gauge ............... 164
8 Local existence for the full Einstein equations ............ 166
8.1 Preservation of the wave gauges ....................... 166
8.2 Geometric local existence ............................. 168
8.3 Geometric uniqueness .................................. 168
8.4 Causality ............................................. 170
9 Constraints in a wave gauge ................................ 172
10 Einstein equations with field sources ...................... 173
10.1 Maxwell constraints ................................... 174
10.2 Lorentz gauge ......................................... 175
10.3 Existence and uniqueness theorems ..................... 176
10.4 Wave equation for F ................................... 177
VII Constraints .............................................. 179
1 Introduction ............................................... 179
2 Linearization and stability ................................ 180
2.1 Linearization of the constraints map, adjoint map ..... 181
2.2 Linearization stability ............................... 183
3 CF (Conformally Formulated) constraints .................... 186
3.1 Hamiltonian constraint ................................ 187
3.2 Momentum constraint ................................... 188
3.3 Scaling of the sources ................................ 189
3.4 Summary of results .................................... 194
3.5 Conformal transformation of the CF constraints ........ 195
3.6 The momentum constraint as an elliptic system ......... 197
4 Case n = 2 ................................................. 200
5 Solutions on compact manifolds ............................. 200
6 Solution of the momentum constraint ........................ 201
7 Lichnerowicz equation ...................................... 204
7.1 The Yamabe classification ............................. 204
7.2 Non-existence and uniqueness .......................... 210
7.3 Existence theorems .................................... 211
8 System of constraints ...................................... 217
8.1 Constant mean curvature r, sources with York-scaled
momentum .............................................. 217
8.2 Solutions with τ wave gauges ................. 162
7.5 Local in time existence in a wave gauge ............... 164
8 Local existence for the full Einstein equations ............ 166
8.1 Preservation of the wave gauges ....................... 166
8.2 Geometric local existence ............................. 168
8.3 Geometric uniqueness .................................. 168
8.4 Causality ............................................. 170
9 Constraints in a wave gauge ................................ 172
10 Einstein equations with field sources ...................... 173
10.1 Maxwell constraints ................................... 174
10.2 Lorentz gauge ......................................... 175
10.3 Existence and uniqueness theorems ..................... 176
10.4 Wave equation for F ................................... 177
VII Constraints .............................................. 179
1 Introduction ............................................... 179
2 Linearization and stability ................................ 180
2.1 Linearization of the constraints map, adjoint map ..... 181
2.2 Linearization stability ............................... 183
3 CF (Conformally Formulated) constraints .................... 186
3.1 Hamiltonian constraint ................................ 187
3.2 Momentum constraint ................................... 188
3.3 Scaling of the sources ................................ 189
3.4 Summary of results .................................... 194
3.5 Conformal transformation of the CF constraints ........ 195
3.6 The momentum constraint as an elliptic system ......... 197
4 Case n = 2 ................................................. 200
5 Solutions on compact manifolds ............................. 200
6 Solution of the momentum constraint ........................ 201
7 Lichnerowicz equation ...................................... 204
7.1 The Yamabe classification ............................. 204
7.2 Non-existence and uniqueness .......................... 210
7.3 Existence theorems .................................... 211
8 System of constraints ...................................... 217
8.1 Constant mean curvature r, sources with York-scaled
momentum .............................................. 217
8.2 Solutions with τ 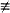 constant or J0 constant or J0 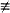 0 ................ 218
9 Solutions on asymptotically Euclidean Manifolds ............ 221
10 Momentum constraint ........................................ 222
11 Solution of the Lichnerowicz equation ...................... 223
11.1 Uniqueness theorem .................................... 223
11.2 Generalized Brill-Cantor theorem ...................... 223
11.3 Existence theorems .................................... 226
12 Solutions of the system of constraints ..................... 229
12.1 Decoupled system ...................................... 229
12.2 Coupled system ........................................ 230
13 Gluing solutions of the constraint equations ............... 232
13.1 Connected sum gluing .................................. 233
13.2 Exterior (Corvino-Schoen) gluing ...................... 235
VIII Other hyperbolic-elliptic well-posed systems ............. 238
1 Introduction ............................................... 238
2 Leray-Ohya non-hyperbolicity of (4)Rij = 0 .................. 238
3 Wave equation for К ........................................ 240
3.1 Hyperbolic system ..................................... 240
3.2 Hyperbolic-elliptic system ............................ 242
4 Fourth-order non-strict and strict hyperbolic systems
for 0 ................ 218
9 Solutions on asymptotically Euclidean Manifolds ............ 221
10 Momentum constraint ........................................ 222
11 Solution of the Lichnerowicz equation ...................... 223
11.1 Uniqueness theorem .................................... 223
11.2 Generalized Brill-Cantor theorem ...................... 223
11.3 Existence theorems .................................... 226
12 Solutions of the system of constraints ..................... 229
12.1 Decoupled system ...................................... 229
12.2 Coupled system ........................................ 230
13 Gluing solutions of the constraint equations ............... 232
13.1 Connected sum gluing .................................. 233
13.2 Exterior (Corvino-Schoen) gluing ...................... 235
VIII Other hyperbolic-elliptic well-posed systems ............. 238
1 Introduction ............................................... 238
2 Leray-Ohya non-hyperbolicity of (4)Rij = 0 .................. 238
3 Wave equation for К ........................................ 240
3.1 Hyperbolic system ..................................... 240
3.2 Hyperbolic-elliptic system ............................ 242
4 Fourth-order non-strict and strict hyperbolic systems
for 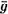 ...................................................... 243
5 First-order hyperbolic systems ............................. 243
5.1 FOSH systems .......................................... 243
6 Bianchi-Einstein equations ................................. 244
6.1 Wave equation for the Riemann tensor .................. 245
6.2 Case n = 3, FOS system ................................ 246
6.3 Cauchy-adapted frame 247
6.4 FOSH system for u = (Е, H, D, В, ...................................................... 243
5 First-order hyperbolic systems ............................. 243
5.1 FOSH systems .......................................... 243
6 Bianchi-Einstein equations ................................. 244
6.1 Wave equation for the Riemann tensor .................. 245
6.2 Case n = 3, FOS system ................................ 246
6.3 Cauchy-adapted frame 247
6.4 FOSH system for u = (Е, H, D, В, 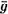 , К, , К, 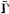 ) ............ 250
6.5 Elliptic-hyperbolic system ............................ 250
7 Bel-Robinson tensor and energy ............................. 254
7.1 The Bel tensor ........................................ 254
7.2 The Bel-Robinson tensor and energy .................... 255
8 Bel-Robinson energy in a strip ............................. 256
IX Relativistic fluids ....................................... 259
1 Introduction ............................................... 259
2 Case of dust ............................................... 260
2.1 Equations ............................................. 260
2.2 Motion of isolated bodies (Choquet-Bruhat and
Friedrichs 2006) ...................................... 262
3 Charged dust ............................................... 263
3.1 Equations ............................................. 263
3.2 Existence and uniqueness theorem in wave and
Lorentz gauges ........................................ 264
3.3 Motion of isolated bodies ............................. 265
4 Perfect fluid, Euler equations ............................. 265
5 Energy properties .......................................... 266
6 Particle number conservation ............................... 267
7 Thermodynamics ............................................. 268
7.1 Definitions. Conservation of entropy .................. 268
7.2 Equations of state .................................... 268
8 Wave fronts, propagation speeds, shocks .................... 270
8.1 General definitions ................................... 270
8.2 Case of perfect fluids ................................ 272
8.3 Shocks ................................................ 273
9 Stationary motion .......................................... 274
10 Dynamic velocity for barotropic fluids ..................... 274
10.1 Fluid index and equations ............................. 274
10.2 Vorticity tensor and Helmholtz equations .............. 276
10.3 Irrotational flows .................................... 277
11 General perfect fluids ..................................... 278
12 Hyperbolic Leray system .................................... 279
12.1 Hyperbolicity of the Euler equations .................. 279
12.2 Reduced Einstein-Euler entropy system ................. 280
12.3 Cauchy problem for the Einstein-Euler
entropy system ................................................ 281
12.4 Motion of isolated bodies ............................. 282
13 First-order symmetric hyperbolic system .................... 282
14 Equations in a flow adapted frame .......................... 284
14.1 n+1 splitting in a time adapted frame ................. 285
14.2 Bianchi equations (case n = 3) ........................ 287
14.3 Vacuum case ........................................... 287
14.4 Perfect fluid ......................................... 288
14.5 Conclusion ............................................ 290
15 Charged fluids ............................................. 290
15.1 Equations ............................................. 290
15.2 Fluids with zero conductivity ......................... 291
16 Fluids with finite conductivity ............................ 293
17 Magnetohydrodynamics ....................................... 294
17.1 Equations ............................................. 294
17.2 Wave fronts ........................................... 295
18 Yang-Mills fluids .......................................... 296
19 Dissipative fluids ......................................... 297
19.1 Viscous fluids ........................................ 297
19.2 The heat equation ..................................... 300
X Relativistic kinetic theory ................................ 301
1 Introduction ............................................... 301
2 Distribution function ...................................... 302
2.1 Definition ............................................ 302
2.2 Interpretation ........................................ 303
2.3 Moments of the distribution function .................. 304
3 Vlasov equations ........................................... 307
3.1 Liouville-Vlasov equation ............................. 307
3.2 Maxwell-Vlasov equation ............................... 310
3.3 Yang-Mills-Vlasov equation ............................ 311
3.4 Particles of a given rest mass ........................ 311
3.5 Conservation of moments ............................... 312
4 Cauchy problem for the Liouville-Vlasov equation ........... 313
4.1 General solution ...................................... 313
4.2 Distribution function on a Robertson-Walker space
time .................................................. 313
4.3 Energy estimates ...................................... 314
4.4 Existence theorem ..................................... 322
4.5 Stress energy tensor of a distribution function ....... 323
5 The Einstein-Vlasov system ................................. 324
5.1 Constraints ........................................... 324
5.2 Cauchy problem for the Einstein equations ............. 325
5.3 Cauchy problem for the coupled system ................. 325
6 The Einstein-Maxwell-Vlasov system ......................... 326
7 Boltzmann equation. Definitions ............................ 328
8 Moments and conservation laws .............................. 329
9 Einstein-Boltzmann system .................................. 331
10 Thermodynamics ............................................. 331
10.1 Entropy and H theorem ................................. 331
10.2 Maxwell-Jüttner equilibrium distribution .............. 333
10.3 Dissipative fluids .................................... 334
11 Extended thermodynamics .................................... 334
11.1 The phenomenological 14 moments theory ................ 335
11.2 Extended thermodynamics of moments .................... 338
11.3 Maximum characteristic velocity ....................... 339
XI Progressive waves ......................................... 341
1 Introduction ............................................... 341
2 Quasilinear systems ........................................ 342
3 Quasilinear first-order systems ............................ 343
3.1 Phase and polarization ................................ 343
3.2 Propagation equations ................................. 344
4 Progressive waves in relativistic fluids ................... 348
4.1 Equations ............................................. 348
4.2 Progressive waves ..................................... 348
4.3 Phases and polarizations .............................. 349
4.4 Polarization and propagation of acoustic waves ........ 351
4.5 Polarization and propagation of matter waves .......... 354
4.6 "Gauge" gravitational waves ........................... 354
5 Quasilinear quasidiagonal second-order systems ............. 354
5.1 Definitions ........................................... 354
5.2 Hyperquasilinear systems with ƒ quadratic in Du ....... 356
5.3 The null condition .................................... 358
6 Non quasidiagonal second-order systems ..................... 359
6.1 Phase and polarization ................................ 360
6.2 Propagation equations ................................. 360
7 Yang-Mills-scalar equations ................................ 361
7.1 Fields and equations .................................. 361
7.2 Phase and polarization ................................ 362
7.3 Propagation ........................................... 363
8 Strong gravitational waves ................................. 364
8.1 Einstein equations .................................... 364
8.2 Phase and polarization ................................ 365
8.3 Propagation and back reaction ......................... 366
8.4 Example ............................................... 368
XII Global hyperbolicity and causality ....................... 371
1 Introduction ............................................... 371
2 Global existence of Lorentzian metrics ..................... 371
3 Time orientation ........................................... 374
4 Futures and pasts .......................................... 375
4.1 Paths and curves ...................................... 375
4.2 Chronology and causality .............................. 375
5 Causal structure of Minkowski spacetime .................... 377
6 Causal structures on general spacetimes .................... 378
7 Geodesic coordinates, normal neighbourhoods ................ 382
8 Topology on a space of paths ............................... 387
8.1 Rectifiable paths ..................................... 387
8.2 Topology on sets of rectifiable paths ................. 388
9 Global hyperbolicity ....................................... 389
9.1 Definition and first criterion ........................ 389
9.2 Maximum of proper length .............................. 390
9.3 Images in V of subsets of ) ............ 250
6.5 Elliptic-hyperbolic system ............................ 250
7 Bel-Robinson tensor and energy ............................. 254
7.1 The Bel tensor ........................................ 254
7.2 The Bel-Robinson tensor and energy .................... 255
8 Bel-Robinson energy in a strip ............................. 256
IX Relativistic fluids ....................................... 259
1 Introduction ............................................... 259
2 Case of dust ............................................... 260
2.1 Equations ............................................. 260
2.2 Motion of isolated bodies (Choquet-Bruhat and
Friedrichs 2006) ...................................... 262
3 Charged dust ............................................... 263
3.1 Equations ............................................. 263
3.2 Existence and uniqueness theorem in wave and
Lorentz gauges ........................................ 264
3.3 Motion of isolated bodies ............................. 265
4 Perfect fluid, Euler equations ............................. 265
5 Energy properties .......................................... 266
6 Particle number conservation ............................... 267
7 Thermodynamics ............................................. 268
7.1 Definitions. Conservation of entropy .................. 268
7.2 Equations of state .................................... 268
8 Wave fronts, propagation speeds, shocks .................... 270
8.1 General definitions ................................... 270
8.2 Case of perfect fluids ................................ 272
8.3 Shocks ................................................ 273
9 Stationary motion .......................................... 274
10 Dynamic velocity for barotropic fluids ..................... 274
10.1 Fluid index and equations ............................. 274
10.2 Vorticity tensor and Helmholtz equations .............. 276
10.3 Irrotational flows .................................... 277
11 General perfect fluids ..................................... 278
12 Hyperbolic Leray system .................................... 279
12.1 Hyperbolicity of the Euler equations .................. 279
12.2 Reduced Einstein-Euler entropy system ................. 280
12.3 Cauchy problem for the Einstein-Euler
entropy system ................................................ 281
12.4 Motion of isolated bodies ............................. 282
13 First-order symmetric hyperbolic system .................... 282
14 Equations in a flow adapted frame .......................... 284
14.1 n+1 splitting in a time adapted frame ................. 285
14.2 Bianchi equations (case n = 3) ........................ 287
14.3 Vacuum case ........................................... 287
14.4 Perfect fluid ......................................... 288
14.5 Conclusion ............................................ 290
15 Charged fluids ............................................. 290
15.1 Equations ............................................. 290
15.2 Fluids with zero conductivity ......................... 291
16 Fluids with finite conductivity ............................ 293
17 Magnetohydrodynamics ....................................... 294
17.1 Equations ............................................. 294
17.2 Wave fronts ........................................... 295
18 Yang-Mills fluids .......................................... 296
19 Dissipative fluids ......................................... 297
19.1 Viscous fluids ........................................ 297
19.2 The heat equation ..................................... 300
X Relativistic kinetic theory ................................ 301
1 Introduction ............................................... 301
2 Distribution function ...................................... 302
2.1 Definition ............................................ 302
2.2 Interpretation ........................................ 303
2.3 Moments of the distribution function .................. 304
3 Vlasov equations ........................................... 307
3.1 Liouville-Vlasov equation ............................. 307
3.2 Maxwell-Vlasov equation ............................... 310
3.3 Yang-Mills-Vlasov equation ............................ 311
3.4 Particles of a given rest mass ........................ 311
3.5 Conservation of moments ............................... 312
4 Cauchy problem for the Liouville-Vlasov equation ........... 313
4.1 General solution ...................................... 313
4.2 Distribution function on a Robertson-Walker space
time .................................................. 313
4.3 Energy estimates ...................................... 314
4.4 Existence theorem ..................................... 322
4.5 Stress energy tensor of a distribution function ....... 323
5 The Einstein-Vlasov system ................................. 324
5.1 Constraints ........................................... 324
5.2 Cauchy problem for the Einstein equations ............. 325
5.3 Cauchy problem for the coupled system ................. 325
6 The Einstein-Maxwell-Vlasov system ......................... 326
7 Boltzmann equation. Definitions ............................ 328
8 Moments and conservation laws .............................. 329
9 Einstein-Boltzmann system .................................. 331
10 Thermodynamics ............................................. 331
10.1 Entropy and H theorem ................................. 331
10.2 Maxwell-Jüttner equilibrium distribution .............. 333
10.3 Dissipative fluids .................................... 334
11 Extended thermodynamics .................................... 334
11.1 The phenomenological 14 moments theory ................ 335
11.2 Extended thermodynamics of moments .................... 338
11.3 Maximum characteristic velocity ....................... 339
XI Progressive waves ......................................... 341
1 Introduction ............................................... 341
2 Quasilinear systems ........................................ 342
3 Quasilinear first-order systems ............................ 343
3.1 Phase and polarization ................................ 343
3.2 Propagation equations ................................. 344
4 Progressive waves in relativistic fluids ................... 348
4.1 Equations ............................................. 348
4.2 Progressive waves ..................................... 348
4.3 Phases and polarizations .............................. 349
4.4 Polarization and propagation of acoustic waves ........ 351
4.5 Polarization and propagation of matter waves .......... 354
4.6 "Gauge" gravitational waves ........................... 354
5 Quasilinear quasidiagonal second-order systems ............. 354
5.1 Definitions ........................................... 354
5.2 Hyperquasilinear systems with ƒ quadratic in Du ....... 356
5.3 The null condition .................................... 358
6 Non quasidiagonal second-order systems ..................... 359
6.1 Phase and polarization ................................ 360
6.2 Propagation equations ................................. 360
7 Yang-Mills-scalar equations ................................ 361
7.1 Fields and equations .................................. 361
7.2 Phase and polarization ................................ 362
7.3 Propagation ........................................... 363
8 Strong gravitational waves ................................. 364
8.1 Einstein equations .................................... 364
8.2 Phase and polarization ................................ 365
8.3 Propagation and back reaction ......................... 366
8.4 Example ............................................... 368
XII Global hyperbolicity and causality ....................... 371
1 Introduction ............................................... 371
2 Global existence of Lorentzian metrics ..................... 371
3 Time orientation ........................................... 374
4 Futures and pasts .......................................... 375
4.1 Paths and curves ...................................... 375
4.2 Chronology and causality .............................. 375
5 Causal structure of Minkowski spacetime .................... 377
6 Causal structures on general spacetimes .................... 378
7 Geodesic coordinates, normal neighbourhoods ................ 382
8 Topology on a space of paths ............................... 387
8.1 Rectifiable paths ..................................... 387
8.2 Topology on sets of rectifiable paths ................. 388
9 Global hyperbolicity ....................................... 389
9.1 Definition and first criterion ........................ 389
9.2 Maximum of proper length .............................. 390
9.3 Images in V of subsets of 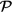 (x, y) ..................... 391
10 Strong and stable causalities .............................. 391
10.1 Strong causality ...................................... 392
10.2 Stable causality ...................................... 392
11 Cauchy surface ............................................. 393
11.1 Domain of dependence. Cauchy horizon .................. 393
11.2 Cauchy surface ........................................ 394
11.3 Global existence of solutions of linear wave
equations ............................................. 397
11.4 Sufficient condition from analysis for global
hyperbolicity ......................................... 397
12 Globally hyperbolic Einsteinian spacetimes ................. 399
12.1 Existence ............................................. 399
12.2 Global uniqueness ..................................... 399
12.3 Examples .............................................. 400
13 Strong cosmic censorship ................................... 400
XIII Singularities ........................................... 402
1 Introduction ............................................... 402
2 Criteria for completeness or incompleteness ................ 404
2.1 A completeness criterion .............................. 404
2.2 An incompleteness criterion ........................... 406
3 Congruence of timelike curves .............................. 408
3.1 Definitions ........................................... 408
3.2 Geodesic deviation .................................... 410
3.3 Raychauduri equation .................................. 411
3.4 Null geodesic congruence .............................. 412
4 First singularity theorem .................................. 412
4.1 Conjugate points ...................................... 412
4.2 Incompleteness theorem ................................ 414
5 Trapped surfaces and singularities ......................... 414
5.1 Trapped surfaces ...................................... 414
5.2 Singularities linked to trapped surfaces .............. 418
6 Black holes ................................................ 418
6.1 Definitions ........................................... 418
6.2 The Hawking area theorem .............................. 420
6.3 The Riemannian Penrose inequality. Case n = 3 ......... 420
7 Weak cosmic censorship conjectures ......................... 421
7.1 Naked singularity ..................................... 421
7.2 Weak cosmic censorship ................................ 422
8 Spherically symmetric Einstein scalar equations ............ 423
8.1 Spherically symmetric spacetimes ...................... 423
8.2 Einstein equations in adapted frame ................... 424
8.3 Reduction to one integro-differential equation ........ 425
8.4 Bondi mass ............................................ 427
8.5 Global existence for small data ....................... 427
8.6 Existence of a global generalized solution for large
data .................................................. 429
8.7 Structure of generalized solutions .................... 432
8.8 Formation of a black hole. Cosmic censorship .......... 433
8.9 Numerical results ..................................... 434
8.10 Instability of naked singularities .................... 434
9 Cosmological singularities. BKL conjecture ................. 435
10 AVTD behaviour ............................................. 441
10.1 Definitions ........................................... 441
10.2 Fuchs theorem ......................................... 441
11 Case of 1-parameter spatial isometry ....................... 443
11.1 Equations ............................................. 443
11.2 VTD solutions of the 2 + 1 Einstein evolution
equations ............................................. 445
11.3 The polarized case .................................... 446
11.4 The unpolarized case .................................. 449
XIV Stationary spacetimes and black holes ................... 451
1 Introduction ............................................... 451
2 Spacetimes with 1-parameter isometry group ................. 452
2.1 Connection and Riemann tensor ......................... 454
2.2 Curvature tensor ...................................... 454
2.3 Ricci tensor .......................................... 455
3 Stationary spacetimes ...................................... 455
3.1 General case .......................................... 455
3.2 Static spacetimes ..................................... 457
4 Gravitational solitons ..................................... 458
4.1 Elementary proofs ..................................... 458
4.2 Case n = 3, Komar mass ................................ 460
5 Electrovac solitons ........................................ 465
6 The Einstein-Yang-Mills case ............................... 466
7 Stationary black holes ..................................... 466
7.1 Definitions ........................................... 466
7.2 Axisymmetry ........................................... 467
8 The rigidity theorem for black holes ....................... 469
9 The Kerr metric and black hole ............................. 471
9.1 Kerr metric in Boyer-Linquist coordinates ............. 471
9.2 The Kerr-Schild spacetime ............................. 472
10 Uniqueness of stationary black holes (dimension 3 + 1) ..... 474
10.1 Static black holes .................................... 475
10.2 Axisymmetric black holes .............................. 475
10.3 Uniqueness of the Kerr black hole ..................... 475
11 Further results ............................................ 476
11.1 Multi black hole solutions ............................ 476
11.2 The Emparan-Reall "black rings" ....................... 478
XV Global existence theorems asymptotically Euclidean data ... 482
1 Introduction ............................................... 482
2 Global existence for small data via the Penrose map ........ 483
2.1 Yang-Mills and associated equations ................... 484
2.2 Quasi-linear wave equations ........................... 484
2.3 Cases n = 3, the null condition ....................... 487
2.4 Wave maps ............................................. 488
3 H. Friedrich conformal system, n + 1 = 4 ................... 488
3.1 Equations ............................................. 488
3.2 Friedrich hyperbolic system ........................... 490
4 Einstein's equations in higher dimensions .................. 491
4.1 Conformal mapping ..................................... 491
4.2 Transformed equations ................................. 492
4.3 Local Cauchy problem in Rxn+1, n ≥ 5 and odd .......... 494
4.4 Global Cauchy problem ................................. 496
4.5 Conclusion ............................................ 497
5 Christodoulou-Klainerman theorem ........................... 497
5.1 CK main theorem ....................................... 497
5.2 Local existence ....................................... 499
5.3 Global existence ...................................... 500
6 The Klainerman-Nicolo theorem .............................. 504
7 The Linblad-Rodnianski theorem ............................. 505
7.1 The Einstein equations in wave coordinates ............ 506
7.2 Initial data .......................................... 507
7.3 Unknowns and norms .................................... 507
7.4 LR theorem ............................................ 508
XVI Global existence theorems the cosmological case .......... 510
1 Introduction ............................................... 510
2 Gowdy cosmological models .................................. 511
3 51 invariant Einsteinian universes, equations .............. 514
3.1 Introduction .......................................... 514
3.2 Definition ............................................ 514
3.3 Equations ............................................. 515
3.4 Twist potential ....................................... 515
3.5 Wave map system ....................................... 516
3.6 Three-dimensional Einstein equations .................. 517
3.7 Teichmuller parameters ................................ 520
4 S1 invariant Einstein universes, Cauchy problem ............ 521
4.1 Cauchy data ........................................... 521
4.2 Construction of A when F is known ..................... 522
4.3 Local in time existence theorem ....................... 522
4.4 Global existence theorem .............................. 522
4.5 Future complete existence ............................. 526
4.6 Einstein-Maxwell-Higgs system ......................... 526
4.7 Conclusion ............................................ 527
5 Andersson-Moncrief theorem ................................. 528
5.1 CMC gauge, elliptic system for N and К ................ 529
5.2 SH gauge, elliptic system for (x, y) ..................... 391
10 Strong and stable causalities .............................. 391
10.1 Strong causality ...................................... 392
10.2 Stable causality ...................................... 392
11 Cauchy surface ............................................. 393
11.1 Domain of dependence. Cauchy horizon .................. 393
11.2 Cauchy surface ........................................ 394
11.3 Global existence of solutions of linear wave
equations ............................................. 397
11.4 Sufficient condition from analysis for global
hyperbolicity ......................................... 397
12 Globally hyperbolic Einsteinian spacetimes ................. 399
12.1 Existence ............................................. 399
12.2 Global uniqueness ..................................... 399
12.3 Examples .............................................. 400
13 Strong cosmic censorship ................................... 400
XIII Singularities ........................................... 402
1 Introduction ............................................... 402
2 Criteria for completeness or incompleteness ................ 404
2.1 A completeness criterion .............................. 404
2.2 An incompleteness criterion ........................... 406
3 Congruence of timelike curves .............................. 408
3.1 Definitions ........................................... 408
3.2 Geodesic deviation .................................... 410
3.3 Raychauduri equation .................................. 411
3.4 Null geodesic congruence .............................. 412
4 First singularity theorem .................................. 412
4.1 Conjugate points ...................................... 412
4.2 Incompleteness theorem ................................ 414
5 Trapped surfaces and singularities ......................... 414
5.1 Trapped surfaces ...................................... 414
5.2 Singularities linked to trapped surfaces .............. 418
6 Black holes ................................................ 418
6.1 Definitions ........................................... 418
6.2 The Hawking area theorem .............................. 420
6.3 The Riemannian Penrose inequality. Case n = 3 ......... 420
7 Weak cosmic censorship conjectures ......................... 421
7.1 Naked singularity ..................................... 421
7.2 Weak cosmic censorship ................................ 422
8 Spherically symmetric Einstein scalar equations ............ 423
8.1 Spherically symmetric spacetimes ...................... 423
8.2 Einstein equations in adapted frame ................... 424
8.3 Reduction to one integro-differential equation ........ 425
8.4 Bondi mass ............................................ 427
8.5 Global existence for small data ....................... 427
8.6 Existence of a global generalized solution for large
data .................................................. 429
8.7 Structure of generalized solutions .................... 432
8.8 Formation of a black hole. Cosmic censorship .......... 433
8.9 Numerical results ..................................... 434
8.10 Instability of naked singularities .................... 434
9 Cosmological singularities. BKL conjecture ................. 435
10 AVTD behaviour ............................................. 441
10.1 Definitions ........................................... 441
10.2 Fuchs theorem ......................................... 441
11 Case of 1-parameter spatial isometry ....................... 443
11.1 Equations ............................................. 443
11.2 VTD solutions of the 2 + 1 Einstein evolution
equations ............................................. 445
11.3 The polarized case .................................... 446
11.4 The unpolarized case .................................. 449
XIV Stationary spacetimes and black holes ................... 451
1 Introduction ............................................... 451
2 Spacetimes with 1-parameter isometry group ................. 452
2.1 Connection and Riemann tensor ......................... 454
2.2 Curvature tensor ...................................... 454
2.3 Ricci tensor .......................................... 455
3 Stationary spacetimes ...................................... 455
3.1 General case .......................................... 455
3.2 Static spacetimes ..................................... 457
4 Gravitational solitons ..................................... 458
4.1 Elementary proofs ..................................... 458
4.2 Case n = 3, Komar mass ................................ 460
5 Electrovac solitons ........................................ 465
6 The Einstein-Yang-Mills case ............................... 466
7 Stationary black holes ..................................... 466
7.1 Definitions ........................................... 466
7.2 Axisymmetry ........................................... 467
8 The rigidity theorem for black holes ....................... 469
9 The Kerr metric and black hole ............................. 471
9.1 Kerr metric in Boyer-Linquist coordinates ............. 471
9.2 The Kerr-Schild spacetime ............................. 472
10 Uniqueness of stationary black holes (dimension 3 + 1) ..... 474
10.1 Static black holes .................................... 475
10.2 Axisymmetric black holes .............................. 475
10.3 Uniqueness of the Kerr black hole ..................... 475
11 Further results ............................................ 476
11.1 Multi black hole solutions ............................ 476
11.2 The Emparan-Reall "black rings" ....................... 478
XV Global existence theorems asymptotically Euclidean data ... 482
1 Introduction ............................................... 482
2 Global existence for small data via the Penrose map ........ 483
2.1 Yang-Mills and associated equations ................... 484
2.2 Quasi-linear wave equations ........................... 484
2.3 Cases n = 3, the null condition ....................... 487
2.4 Wave maps ............................................. 488
3 H. Friedrich conformal system, n + 1 = 4 ................... 488
3.1 Equations ............................................. 488
3.2 Friedrich hyperbolic system ........................... 490
4 Einstein's equations in higher dimensions .................. 491
4.1 Conformal mapping ..................................... 491
4.2 Transformed equations ................................. 492
4.3 Local Cauchy problem in Rxn+1, n ≥ 5 and odd .......... 494
4.4 Global Cauchy problem ................................. 496
4.5 Conclusion ............................................ 497
5 Christodoulou-Klainerman theorem ........................... 497
5.1 CK main theorem ....................................... 497
5.2 Local existence ....................................... 499
5.3 Global existence ...................................... 500
6 The Klainerman-Nicolo theorem .............................. 504
7 The Linblad-Rodnianski theorem ............................. 505
7.1 The Einstein equations in wave coordinates ............ 506
7.2 Initial data .......................................... 507
7.3 Unknowns and norms .................................... 507
7.4 LR theorem ............................................ 508
XVI Global existence theorems the cosmological case .......... 510
1 Introduction ............................................... 510
2 Gowdy cosmological models .................................. 511
3 51 invariant Einsteinian universes, equations .............. 514
3.1 Introduction .......................................... 514
3.2 Definition ............................................ 514
3.3 Equations ............................................. 515
3.4 Twist potential ....................................... 515
3.5 Wave map system ....................................... 516
3.6 Three-dimensional Einstein equations .................. 517
3.7 Teichmuller parameters ................................ 520
4 S1 invariant Einstein universes, Cauchy problem ............ 521
4.1 Cauchy data ........................................... 521
4.2 Construction of A when F is known ..................... 522
4.3 Local in time existence theorem ....................... 522
4.4 Global existence theorem .............................. 522
4.5 Future complete existence ............................. 526
4.6 Einstein-Maxwell-Higgs system ......................... 526
4.7 Conclusion ............................................ 527
5 Andersson-Moncrief theorem ................................. 528
5.1 CMC gauge, elliptic system for N and К ................ 529
5.2 SH gauge, elliptic system for 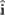 and β ................. 529
5.3 The Bianchi equations ................................. 530
5.4 Existence theorems .................................... 531
5.5 Global existence theorem .............................. 532
6 Einstein non-linear scalar field system .................... 533
APPENDICES
I Sobolev spaces on Riemannian manifolds ..................... 534
1 Definitions ................................................ 534
2 Embedding and multiplication properties .................... 535
2.1 Open subsets of Rn .................................... 535
2.2 Riemannian manifolds .................................. 536
3 Weighted Sobolev spaces .................................... 537
3.1 Definitions ........................................... 537
3.2 Embedding and multiplication properties ............... 538
II Second-order elliptic systems on Riemannian manifolds ..... 542
1 Linear elliptic systems .................................... 542
2 Linear elliptic systems on compact M ....................... 544
2.1 General second-order systems .......................... 544
2.2 Poisson operator ...................................... 551
2.3 Conformal Laplace operator ............................ 552
3 Asymptotically Euclidean manifolds ......................... 553
3.1 Definitions ........................................... 553
3.2 Second-order linear elliptic systems .................. 554
4 Special systems ............................................ 560
4.1 Poisson operator ...................................... 560
4.2 Conformal Laplace operator ............................ 561
5 Equation Δγφ = ƒ(x,φ), compact M ........................... 562
6 Δγφ = ƒ(x,φ) on (M, γ) asymptotically Euclidean ............ 567
III Quasi-diagonal, quasi-linear, second-order hyperbolic
systems .................................................. 571
1 Introduction ............................................... 571
2 Wave equation on (V, g) .................................... 571
2.1 Definitions ........................................... 572
2.2 Stress energy tensor. Energy momentum vector .......... 572
2.3 Energy density ........................................ 574
2.4 Energy equality on a compact domain ................... 575
2.5 Energy inequality in a compact causal domain .......... 578
2.6 Uniqueness theorem and causality ...................... 580
2.7 Case of a strip ....................................... 581
2.8 Estimate of u ......................................... 582
2.9 Cauchy problem ........................................ 583
2.10 Generalizations ....................................... 589
3 Quasidiagonal linear systems ............................... 590
3.1 Definitions ........................................... 590
3.2 Stress energy tensor .................................. 590
3.3 Energy inequality in a compact causal domain .......... 591
3.4 Case of a strip VT .................................... 592
3.5 Existence, uniqueness, causality and continuity ....... 594
3.6 Higher order estimates ................................ 594
3.7 Other hypotheses on g ................................. 600
3.8 Cauchy data in local spaces ........................... 601
4 Quasilinear systems ........................................ 604
4.1 Semilinear systems .................................... 604
4.2 Further results for semilinear equations .............. 607
4.3 Quasilinear systems ................................... 608
5 Global existence ........................................... 613
5.1 Semilinear systems .................................... 613
5.2 Quasilinear equations ................................. 616
IV General hyperbolic systems ................................. 617
1 Introduction ............................................... 617
2 Leray hyperbolic systems ................................... 617
2.1 Case of one equation .................................. 617
2.2 Leray hyperbolic systems .............................. 622
3 Leray-Ohya hyperbolic systems .............................. 624
4 First-order symmetric hyperbolic systems ................... 625
4.1 FOSH systems on Rn+1 .................................. 625
4.2 FOSH systems on a sliced manifold ..................... 627
V Cauchy—Kovalevski and Fuchs theorems ....................... 631
1 Introduction ............................................... 631
2 Cauchy-Kovalevski theorem .................................. 631
2.1 Linear system ......................................... 631
2.2 Non-linear system ..................................... 634
3 Fuchs theorem .............................................. 634
3.1 Definitions ........................................... 634
3.2 Theorem ............................................... 636
3.3 Equivalence with an integral equation ................. 637
3.4 Equivalence with another mapping ...................... 638
3.5 Convergence of iterations ............................. 641
3.6 Global in space theorem ............................... 642
VI Conformal methods ......................................... 643
1 Introduction ............................................... 643
2 Conformal metrics. Confomorphisms .......................... 643
2.1 Connections of conformal metrics ...................... 643
2.2 Riemann tensors of conformal metrics .................. 644
2.3 Ricci tensors of conformal metrics .................... 644
3 The Weyl tensor ............................................ 645
4 Conformal transformations of field equations ............... 646
4.1 Maxwell and Yang-Mills equations ...................... 646
5 Invariance of wave equations ............................... 647
6 Penrose transform .......................................... 647
7 Einstein spaces with cosmological constant ................. 650
7.1 Conformal transformation of De Sitter spacetime ....... 650
7.2 Conformal transformation of anti-De Sitter
spacetime ............................................. 650
8 Asymptotically simple spacetimes ........................... 650
8.1 Conformal compactifications ........................... 650
8.2 Black holes ........................................... 652
VII Kaluza—Klein theories .................................... 653
1 Introduction ............................................... 653
2 Isometries ................................................. 653
3 Kaluza-Klein metrics ....................................... 654
3.1 Metric in adapted frame ............................... 654
3.2 Structure coefficients ................................ 655
3.3 Kaluza-Klein connection ............................... 656
4 Curvature tensor ........................................... 657
5 Ricci tensor and K-K equations ............................. 659
6 Equations in conformal spacetime metric .................... 660
RELATED PAPERS
Causality of classical supergravity ........................ 665
Lecture Notes in Physics 1986, E. Flaherty ed.
Springer 61-84
Gravitation with gauss bonnet terms ........................ 689
Australian National University Publications 1988
R. Bartnik ed. 53-72
Interaction of gravitational and fluid waves ............... 709
In collaboration with A. Greco, Cericolo nat. di Paleruno
1994 Serie II n° 45, III. 123
Positive-energy theorems ................................... 723
Relativity, Group and Topology II, В. Dewitt and R. Stora
ed. 742-786
REFERENCES .................................................... 771
INDEX ......................................................... 781 and β ................. 529
5.3 The Bianchi equations ................................. 530
5.4 Existence theorems .................................... 531
5.5 Global existence theorem .............................. 532
6 Einstein non-linear scalar field system .................... 533
APPENDICES
I Sobolev spaces on Riemannian manifolds ..................... 534
1 Definitions ................................................ 534
2 Embedding and multiplication properties .................... 535
2.1 Open subsets of Rn .................................... 535
2.2 Riemannian manifolds .................................. 536
3 Weighted Sobolev spaces .................................... 537
3.1 Definitions ........................................... 537
3.2 Embedding and multiplication properties ............... 538
II Second-order elliptic systems on Riemannian manifolds ..... 542
1 Linear elliptic systems .................................... 542
2 Linear elliptic systems on compact M ....................... 544
2.1 General second-order systems .......................... 544
2.2 Poisson operator ...................................... 551
2.3 Conformal Laplace operator ............................ 552
3 Asymptotically Euclidean manifolds ......................... 553
3.1 Definitions ........................................... 553
3.2 Second-order linear elliptic systems .................. 554
4 Special systems ............................................ 560
4.1 Poisson operator ...................................... 560
4.2 Conformal Laplace operator ............................ 561
5 Equation Δγφ = ƒ(x,φ), compact M ........................... 562
6 Δγφ = ƒ(x,φ) on (M, γ) asymptotically Euclidean ............ 567
III Quasi-diagonal, quasi-linear, second-order hyperbolic
systems .................................................. 571
1 Introduction ............................................... 571
2 Wave equation on (V, g) .................................... 571
2.1 Definitions ........................................... 572
2.2 Stress energy tensor. Energy momentum vector .......... 572
2.3 Energy density ........................................ 574
2.4 Energy equality on a compact domain ................... 575
2.5 Energy inequality in a compact causal domain .......... 578
2.6 Uniqueness theorem and causality ...................... 580
2.7 Case of a strip ....................................... 581
2.8 Estimate of u ......................................... 582
2.9 Cauchy problem ........................................ 583
2.10 Generalizations ....................................... 589
3 Quasidiagonal linear systems ............................... 590
3.1 Definitions ........................................... 590
3.2 Stress energy tensor .................................. 590
3.3 Energy inequality in a compact causal domain .......... 591
3.4 Case of a strip VT .................................... 592
3.5 Existence, uniqueness, causality and continuity ....... 594
3.6 Higher order estimates ................................ 594
3.7 Other hypotheses on g ................................. 600
3.8 Cauchy data in local spaces ........................... 601
4 Quasilinear systems ........................................ 604
4.1 Semilinear systems .................................... 604
4.2 Further results for semilinear equations .............. 607
4.3 Quasilinear systems ................................... 608
5 Global existence ........................................... 613
5.1 Semilinear systems .................................... 613
5.2 Quasilinear equations ................................. 616
IV General hyperbolic systems ................................. 617
1 Introduction ............................................... 617
2 Leray hyperbolic systems ................................... 617
2.1 Case of one equation .................................. 617
2.2 Leray hyperbolic systems .............................. 622
3 Leray-Ohya hyperbolic systems .............................. 624
4 First-order symmetric hyperbolic systems ................... 625
4.1 FOSH systems on Rn+1 .................................. 625
4.2 FOSH systems on a sliced manifold ..................... 627
V Cauchy—Kovalevski and Fuchs theorems ....................... 631
1 Introduction ............................................... 631
2 Cauchy-Kovalevski theorem .................................. 631
2.1 Linear system ......................................... 631
2.2 Non-linear system ..................................... 634
3 Fuchs theorem .............................................. 634
3.1 Definitions ........................................... 634
3.2 Theorem ............................................... 636
3.3 Equivalence with an integral equation ................. 637
3.4 Equivalence with another mapping ...................... 638
3.5 Convergence of iterations ............................. 641
3.6 Global in space theorem ............................... 642
VI Conformal methods ......................................... 643
1 Introduction ............................................... 643
2 Conformal metrics. Confomorphisms .......................... 643
2.1 Connections of conformal metrics ...................... 643
2.2 Riemann tensors of conformal metrics .................. 644
2.3 Ricci tensors of conformal metrics .................... 644
3 The Weyl tensor ............................................ 645
4 Conformal transformations of field equations ............... 646
4.1 Maxwell and Yang-Mills equations ...................... 646
5 Invariance of wave equations ............................... 647
6 Penrose transform .......................................... 647
7 Einstein spaces with cosmological constant ................. 650
7.1 Conformal transformation of De Sitter spacetime ....... 650
7.2 Conformal transformation of anti-De Sitter
spacetime ............................................. 650
8 Asymptotically simple spacetimes ........................... 650
8.1 Conformal compactifications ........................... 650
8.2 Black holes ........................................... 652
VII Kaluza—Klein theories .................................... 653
1 Introduction ............................................... 653
2 Isometries ................................................. 653
3 Kaluza-Klein metrics ....................................... 654
3.1 Metric in adapted frame ............................... 654
3.2 Structure coefficients ................................ 655
3.3 Kaluza-Klein connection ............................... 656
4 Curvature tensor ........................................... 657
5 Ricci tensor and K-K equations ............................. 659
6 Equations in conformal spacetime metric .................... 660
RELATED PAPERS
Causality of classical supergravity ........................ 665
Lecture Notes in Physics 1986, E. Flaherty ed.
Springer 61-84
Gravitation with gauss bonnet terms ........................ 689
Australian National University Publications 1988
R. Bartnik ed. 53-72
Interaction of gravitational and fluid waves ............... 709
In collaboration with A. Greco, Cericolo nat. di Paleruno
1994 Serie II n° 45, III. 123
Positive-energy theorems ................................... 723
Relativity, Group and Topology II, В. Dewitt and R. Stora
ed. 742-786
REFERENCES .................................................... 771
INDEX ......................................................... 781
|