Preface ........................................................ ix
1 Preliminaries
1.1 Banach space-valued measures ............................ 1
1.2 lcHs-valued measures ................................... 11
2 Basic Properties of the Bartle-Dunford-Schwartz Integral
2.1 (KL) m-integrability ................................... 17
2.2 (BDS) m-integrability .................................. 26
3  p-spaces, 1 ≤ p ≤ ∞
3.1 The seminorms m•p(•,T) on p-spaces, 1 ≤ p ≤ ∞
3.1 The seminorms m•p(•,T) on  p p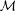 (m), 1 ≤ p < ∞ ........... 33
3.2 Completeness of (m), 1 ≤ p < ∞ ........... 33
3.2 Completeness of  p p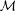 (m) and (m) and  p p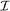 (m), 1 ≤ p < ∞, (m), 1 ≤ p < ∞,  ∞(m) ... 42
3.3 Characterizations of ∞(m) ... 42
3.3 Characterizations of  p p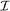 (m), 1 ≤ p < ∞ ................. 47
3.4 Other convergence theorems for (m), 1 ≤ p < ∞ ................. 47
3.4 Other convergence theorems for  p(m), 1 ≤ p < ∞ ........ 54
3.5 Relations between the spaces p(m), 1 ≤ p < ∞ ........ 54
3.5 Relations between the spaces  p(m) ..................... 63
4 Integration With Respect to IcHs-valued Measures
4.1 (KL) m-integrability (m lcHs-valued) ................... 65
4.2 (BDS) m-integrability (m lcHs-valued) .................. 78
4.3 The locally convex spaces p(m) ..................... 63
4 Integration With Respect to IcHs-valued Measures
4.1 (KL) m-integrability (m lcHs-valued) ................... 65
4.2 (BDS) m-integrability (m lcHs-valued) .................. 78
4.3 The locally convex spaces  p p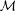 (m), (m),  p p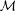 (σ(Ρ),m), (σ(Ρ),m),
 p p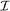 (m) and (m) and  p p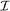 (σ(Ρ),m), 1 ≤ p < ∞ ...................... 85
4.4 Completeness of (σ(Ρ),m), 1 ≤ p < ∞ ...................... 85
4.4 Completeness of  p p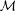 (m), (m),  p p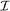 (m), (m),  p p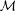 (σ(Ρ),m) and (σ(Ρ),m) and
 p p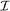 (σ(Ρ),m), for suitable X ............................ 91
4.5 Characterizations of (σ(Ρ),m), for suitable X ............................ 91
4.5 Characterizations of  p-spaces, convergence
theorems and relations between p-spaces, convergence
theorems and relations between  p-spaces .............. 101
4.6 Separability of p-spaces .............. 101
4.6 Separability of  p(m) and p(m) and  p(σ(Ρ),m), 1 ≤ p < ∞,
m IcHs-valued ......................................... 109
5 Applications to Integration in Locally Compact Hausdorff
Spaces - Part I
5.1 Generalizations of the Vitali-Carathéodory
Integrability Criterion Theorem ....................... 117
5.2 The Baire version of the Dieudonné-Grothendieck
theorem and its vector-valued generalizations ......... 121
5.3 Weakly compact bounded Radon operators and
prolongable Radon operators ........................... 138
6 Applications to Integration in Locally Compact Hausdorff
Spaces - Part II
6.1 Generalized Lusin's Theorem and its variants .......... 153
6.2 Lusin measurability of functions and sets ............. 159
6.3 Theorems of integrability criteria .................... 165
6.4 Additional convergence theorems ....................... 187
6.5 Duals of p(σ(Ρ),m), 1 ≤ p < ∞,
m IcHs-valued ......................................... 109
5 Applications to Integration in Locally Compact Hausdorff
Spaces - Part I
5.1 Generalizations of the Vitali-Carathéodory
Integrability Criterion Theorem ....................... 117
5.2 The Baire version of the Dieudonné-Grothendieck
theorem and its vector-valued generalizations ......... 121
5.3 Weakly compact bounded Radon operators and
prolongable Radon operators ........................... 138
6 Applications to Integration in Locally Compact Hausdorff
Spaces - Part II
6.1 Generalized Lusin's Theorem and its variants .......... 153
6.2 Lusin measurability of functions and sets ............. 159
6.3 Theorems of integrability criteria .................... 165
6.4 Additional convergence theorems ....................... 187
6.5 Duals of  1(m) and 1(m) and  1(n) .............................. 202
7 Complements to the Thomas Theory
7.1 Integration of complex functions with respect
to a Radon operator ................................... 213
7.2 Integration with respect to a weakly compact bounded
Radon operator ........................................ 221
7.3 Integration with respect to a prolongable Radon
operator .............................................. 233
7.4 Baire versions of Proposition 4.8 and Theorem 4.9
of [T] ................................................ 241
7.5 Weakly compact and prolongable Radon vector
measures .............................................. 251
7.6 Relation between 1(n) .............................. 202
7 Complements to the Thomas Theory
7.1 Integration of complex functions with respect
to a Radon operator ................................... 213
7.2 Integration with respect to a weakly compact bounded
Radon operator ........................................ 221
7.3 Integration with respect to a prolongable Radon
operator .............................................. 233
7.4 Baire versions of Proposition 4.8 and Theorem 4.9
of [T] ................................................ 241
7.5 Weakly compact and prolongable Radon vector
measures .............................................. 251
7.6 Relation between  p(u) and p(u) and  p(mu), u a weakly
compact bounded Radon operator or a prolongable
Radon operator ........................................ 275
Bibliography .................................................. 287
Acknowledgment ................................................ 293
List of Symbols ............................................... 295
Index ......................................................... 297 p(mu), u a weakly
compact bounded Radon operator or a prolongable
Radon operator ........................................ 275
Bibliography .................................................. 287
Acknowledgment ................................................ 293
List of Symbols ............................................... 295
Index ......................................................... 297
|